4-9. 無限小回転

4-9-1. オイラーの定理

球面上に拘束された剛体運動は, 球の中心まわりの回転変位で表される. 回転変位に関しては, ｢点のまわりの回転変位は, その点を通る1つの軸のまわりの回転によって達せられる｣ が成立する. これをオイラーの定理という.

証明: 点$O$を中心とする半径1の単位球を想定する (図20) . 球面上の2点$A$, $B$が点$O$を回転の中心として剛体回転によってそれぞれ$A'$, $B'$に変位したとする. 大円の弧$AA'$および$BB'$を垂直に2等分する大円の交点を$C$とすると, 大円の弧$AC$と$A'C$の長さは等しく, また$BC$と$B'C$の長さは等しい. 剛体だから$AB$と$A'B'$の長さは等しいので, 球面三角形$ABC$と$A'B'C$は合同である. 従って, 上記の剛体回転は, 軸$OC$のまわりの角度$∠ACA' (＝∠BCB')$だけの回転によって表される.

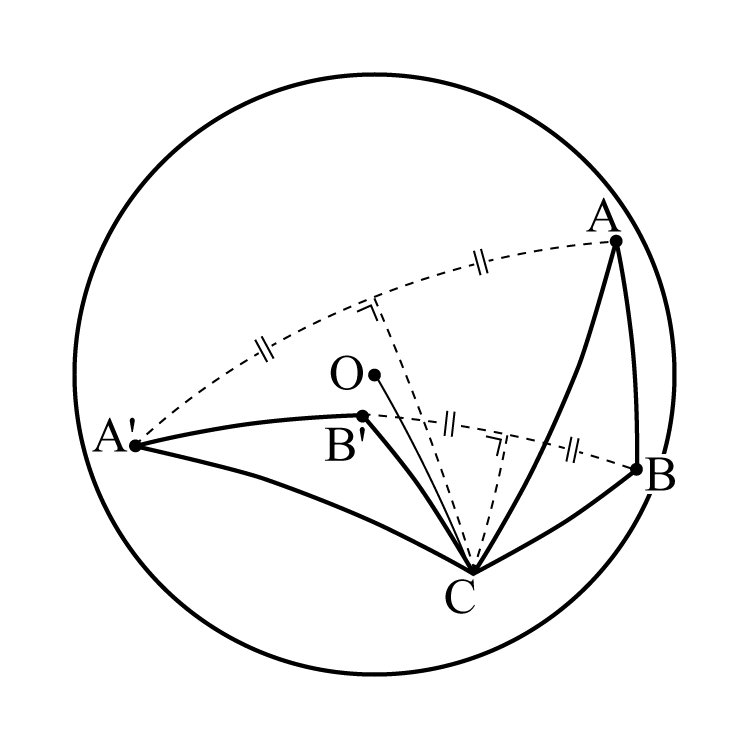
図1

4-9-2. 有限回転の非ベクトル性

オイラーの定理により, 剛体の回転変位は大きさと向きをもつ. すなわち, 回転角の大きさを絶対値にもち, 向きは右ねじの規約に従う有向量である. しかし, 図21に示すように, 有限の大きさをもつ回転変位を複数合成したとき, 和に関する交換法則は成立しない. 従って, 有限回転はベクトルではない.

例: 直交するx軸とy軸のまわりのそれぞれ$90^\circ$の回転を考える. 最初にx軸まわり, 続いてy軸まわりの回転を行った場合と, 順序を逆にした場合とで, 結果が異なる (図21) .

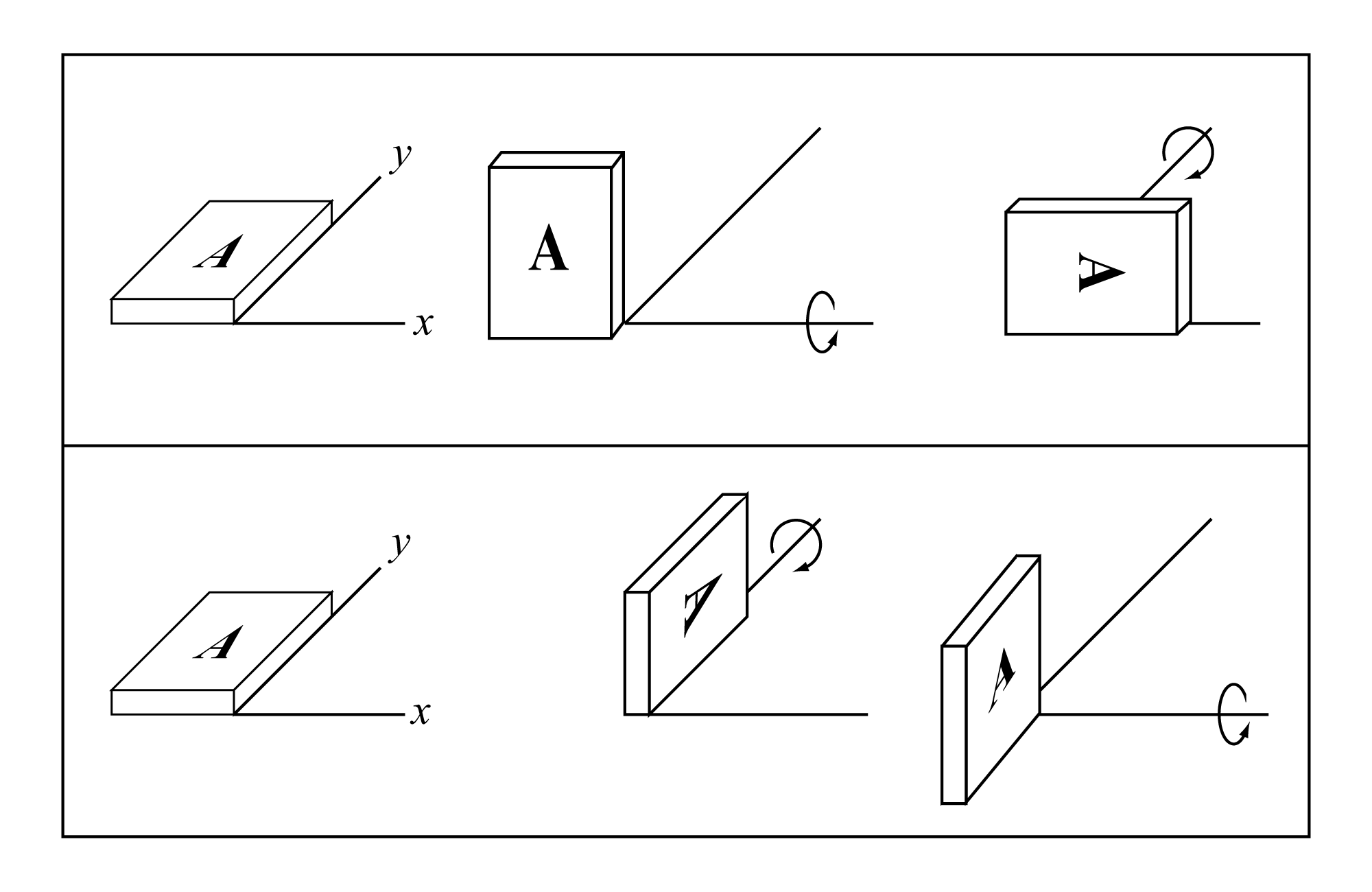
図2

4-9-3. 無限小回転のベクトル性

2次以上の高次の項を無視できる回転を無限小回転と呼ぶ. 点$O$を通る軸$OA$まわりの無限小剛体回転を考える. これを微小な大きさ$\epsilon$をもち, $OA$方向を向く有向量$\boldsymbol{\epsilon}$で表す. 剛体内の質点$P$ (位置ベクトル$\boldsymbol{r}$) が無限小回転によって点$P'$ (位置ベクトル$\boldsymbol{r'}$) に変位したとすると (図22) , その変位ベクトル$\Delta \boldsymbol{r} ＝ \boldsymbol{r'} - \boldsymbol{r}$ の大きさは軸$OA$と$\boldsymbol{r}$のなす角$\theta$を用いて近似的に$\epsilon r \sin\theta$に等しい. ベクトル積の記号を用いると

\[ \Delta \boldsymbol{r} = \boldsymbol{r'} - \boldsymbol{r} = \boldsymbol{\epsilon} \times \boldsymbol{r} + o(\epsilon^2) \tag{1} \]

となる. すなわち, 位置$\boldsymbol{r}$にあった質点は無限小回転$\boldsymbol{\epsilon}$によって

\[ \boldsymbol{r'} = \boldsymbol{r} + \boldsymbol{\epsilon} \times \boldsymbol{r} + o(\epsilon^2) \tag{2} \]

で与えられる位置$r'$に移る. さらに, 別の軸$OB$まわりの無限小回転$\boldsymbol{\epsilon}'$を行うものとする. 質点は点$P'$から点$P''$ (位置ベクトル$r''$) へ移り

\[ \boldsymbol{r''} = \boldsymbol{r'} + \boldsymbol{\epsilon '} \times \boldsymbol{r'} + o(\epsilon^2) \tag{3} \]

が成り立つ.

(9-3) 式をを (9-2) 式に代入すると

\[ \boldsymbol{r''} = \boldsymbol{r} + \left(\boldsymbol{\epsilon} + \boldsymbol{\epsilon '} \right) \times \boldsymbol{r} + o(\epsilon^2, \epsilon \epsilon ', \epsilon '^2) \tag{4} \]

となる.

つまり, 2次以上の高次の項が無視できる無限小回転$\epsilon$と$\epsilon '$を連続して行ったものは, 両者をベクトル的に合成した無限小回転$(\epsilon ＋ \epsilon ')$を一挙に行ったのと同等である. 順序を逆にしても同じ結果が得られる. すなわち, 無限小回転はベクトルとして扱うことができる.

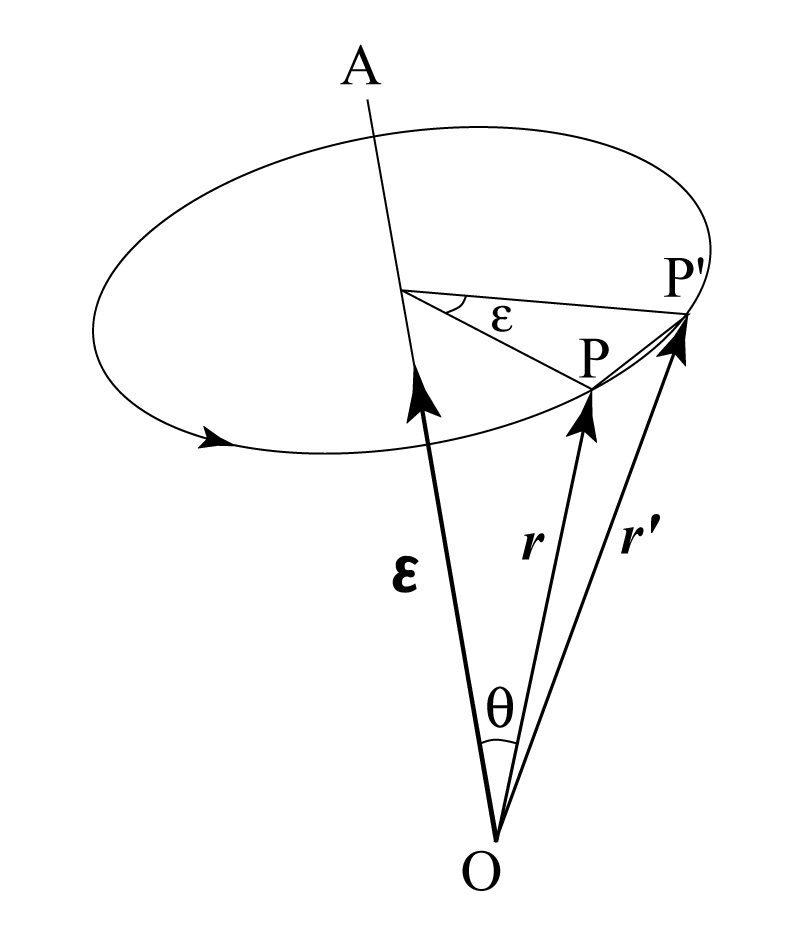
図2

4-9-4. 無限小回転の角速度と質点の速度

時間を細かく分割してみれば, 有限回転は無限小回転の積み重ねとみなすことができる. 時刻$t$から$t+\Delta t$までの短い時間間隔の間に剛体が行う無限小回転を

\[ \epsilon = \boldsymbol{\omega} \Delta t \tag{5} \]

とすると, $\boldsymbol{\omega}$は時刻$t$における瞬間の角速度を与えるベクトルであり, その向きは瞬間の回転軸方向と同じである.

(5) 式を (1) 式に代入すると

\[ \Delta r = \boldsymbol{\omega} \times \boldsymbol{r} \Delta t +o(\epsilon^2) \tag{6} \]

となるので, 質点の速度$\boldsymbol{v}$は

\[ \boldsymbol{v} = \frac{d \boldsymbol{r}}{dt} = \boldsymbol{\omega} \times \boldsymbol{r} \tag{7} \]

で与えられる.

4-9-5. 短い時間スケールのプレート運動

プレート運動の速度は, プレート間の相対運動においても, 地球深部に対する絶対運動においても, 高々10cm/yrの大きさである. この大きさは地球半径に比べ十分小さく, 短い時間スケールのプレート運動は無限小回転として扱うことができる.

3つのプレートA, B, Cを想定し, プレートAに対するプレートBの無限小回転の角速度ベクトルを$_B\omega_A$, 同様にプレートBに対するプレートCの無限小回転の角速度ベクトルを$_C\omega_B$と表す. 4-9-3で述べたように, これらはベクトルとして合成できる. 結果は足し算の順序によらない. すなわち, プレートAに対してBを無限小回転させ, 次にBに対してCを無限小回転させたものは, 最初にプレートBに対してCを回転させ, 次にAに対してBとCを同時に回転させた結果に一致する. これらはいずれもプレートAに対するプレートCの無限小回転を表し, オイラーの定理により, ただひとつの回転$_C\omega_A$によって表される.

\[ _C\omega_A = _C\omega_B + _B\omega_A \tag{8} \]

(8) 式は, プレートAとB, プレートBとCの間の相対運動が既知であれば, 両者を合成することで, プレートAとCの間の相対運動を求めることができることを意味する.

長期間のプレート運動を扱うときは事情が異なる. 仮に10 cm/yrの速度でプレート運動が10万年間続いたとすると, 積算移動量は10 kmとなる. 地球半径に比べまだ十分小さい値なので, 無限小回転としての扱いが可能であろう. 一方, 同じ速度で運動が1000万年間続けば, 積算移動量は1000 kmに達し, もはや無限小回転ではなく, 有限回転の扱いが必要である. 後者の場合には, 4-9-2で述べたように, 和の交換法則は成り立たない.

参考文献

喜多秀次ほか (1974) :基礎物理コース－力学, 学術図書出版

その他にも適当な力学の教科書が多数ある.