粘弾性変形の理論とその進展

東京大学地震研究所田中愛幸

1. 粘弾性の基礎

弾性とは, 加えられた力に比例して変形(伸びや縮み)が生じ, 力を取り除くと元の形に戻る性質のことをいう. 粘性とは, 力を加えている間は変形が増大し, 力を取り除いても元に戻らないような性質をいう. 両者を合わせた性質を粘弾性という.

一次元的な固体を考えて, $\tau$を応力, $x$を伸び(変位), $ｋ$を弾性定数(Pa), $\mu$を粘性(Pa s)とすると, 弾性はフックの法則($\tau=kx$), 粘性はニュートンの法則($\tau=\mu dx/dt$)で記述できる. 弾性はバネ, 粘性はダッシュポットに対応していると考えればよい. これらを直列につないだものをマックスウェルの粘弾性モデルと呼ぶ(図１). 時刻$t=0$に時間変化しない一定の変位を与えると, バネは$t=0$で瞬時に伸びるが, ダッシュポットの変位量はゼロである. t>0では, バネに蓄えられた弾性エネルギーがダッシュポットの変位によって消費され, バネの伸びがゼロになるまでダッシュポットの変位が継続する. これを応力緩和という. ダッシュポットの変位量は$1-\exp(-(k/\mu ) t)$に比例し, $\mu /k$は緩和時間と呼ばれる.

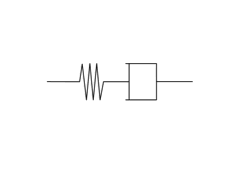
図1. マックスウェルの粘弾性モデル

2. マントルの粘弾性とポストグレイシャルリバウンド

マントル対流という用語があるように, 非常に長い時間スケール(例えば数千万年)では, マントルは粘性流体のように振る舞う. 一方, マントル中を地震波が伝わることから明らかなように, 短い時間スケール(例えば数時間)ではマントルは弾性体として振る舞う. それでは, その間の時間スケールでは, マントルは粘弾性的性質を示すのだろうか？

スカンジナビア半島や北米大陸等に大規模な氷床が存在したことが知られている. これらの地域では, 年間1 cm以上の隆起が発生していることが測地観測によって捉えられている(Sella et al. 2007). この現象はポストグレイシャルリバウンド(Post Glacial Rebound或いはグレイシャルアイソスタティックアジャストメントGlacial Isostatic Adjustment)と呼ばれ, 粘弾性変形の理論で説明することができる. 地球表層に存在した氷の荷重によってマントルにまで及んでいた(弾性体としての)地殻の凹みが, 氷床が消失した今も少しずつ回復してきている.

氷床の時空間分布を入力とする粘弾性変形モデルを構築し, 現在の隆起速度と一致するようにマントルの粘性構造を決めることができる(Peltier, 1998). 下部マントルの平均的な粘性は1020-21 Pasで, 緩和時間でいうと数千年になる. このような長い時間スケールの岩石の振る舞いを実験室で精度よく調べることは難しく, 今述べたような観測とモデルとの比較に依らざるを得ない.

3. 地震の余効変動と粘弾性

固体地球の粘弾性を示す現象は他にもある. 図２は関東地震前後の油壺験潮所の潮位を示す(Thatcher & Rundle, 1979). 地震により三浦半島が隆起したので潮位が下がり, その後, 地震前と異なる速度で戻ってきている. これは次のように解釈できる. 地震により地殻やマントルに急激な応力変化が生じ変形が起きる. 地球が弾性体であればそれで変形は終了だが, 地殻下部や上部マントルに加わった応力は, 粘性のために徐々に緩和していく. このように地震後, 数10年以上も続くような余効変動は他の大地震でも捉えられている.

物理モデルもポストグレイシャルリバウンドと同じように構築できる. 境界条件は, 地球表面は荷重がないので自由表面とし, 断層面の位置には変位のくいちがいを$t>=0$に与える. モデルと観測値の比較から, 地殻下部や上部マントルの粘性は1018-19 Pasのオーダーに求まることが多い. 余効変動はポストグレイシャルリバウンドよりも変形の空間スケールが小さいため, プレート境界浅部のより局地的な粘性を反映していると考えられる.

余効すべりやゆっくり地震と異なり, 粘弾性余効変動は断層すべりによって生じる変形ではない. しかしながら, 間接的に断層面の固着の推定に関係する. インターサイスミック期の地殻変動を解釈する際, 過去の大地震による粘弾性変形の寄与を適切に取り除かないと, 固着の過小/過大評価してしまう可能性がある. また, 粘性を正しく推定することで, 大地震のサイクルにおける応力の時空間変化を精度よくシミュレートすることができる. このような意味で, 地震後の余効変動の観測とモデリングは, 地震サイクルの定量的な理解のために重要である.

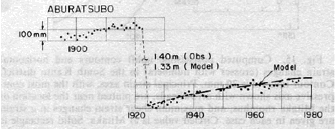
図2. 関東地震前後の油壺の潮位

4. 粘弾性余効変動と超巨大地震

モデルと観測値を比較して推定する粘性は, 当然ながらモデルの諸要素(半無限媒質にするか成層構造にするか, ３次元的な粘弾性・密度構造を考慮するか, 重力の効果も含めるか等)にも依存する. 様々な研究者がより現実に近いモデルを考案してきており, 近年は有限要素法の利用も多い(e.g. Suito and Hirahara, 1999, Tanaka et al., 2011 ).

最近, 超巨大地震による数100kmスケールの変形を解釈するために, 地球の曲率を考慮したモデルの必要性が高まっている. 曲率や重力の効果をより自然な形で扱うには, 地球を球体としたモデルが適している(田中, 2013). これまで粘弾性余効変動を球体で扱うには数理的な困難が存在していたが, いくつかの回避方法が提案されている(Tanaka et al., 2007, Tanaka et al., 2011). 曲率の影響を加味するだけでなく, 球体モデルはGRACEによる衛星重力データとの比較も容易なため, 地上GNSS観測では空間分解能が限られるような海域周辺で発生する超巨大地震のメカニズムを推定するのに威力を発揮する. 図は, ２００４年スマトラ大地震後の重力変化が粘弾性余効果変動でよく説明できることを示している.

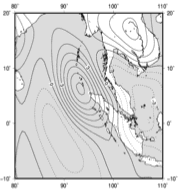
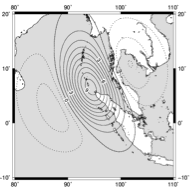
図3. ２００４年スマトラ大地震による地震後の重力変化(Tanaka et al., 2014). 左:GRACE衛星重力ミッションによる観測値. ２００５年と２０１１年の平均値の差. 単位はmicroGal. 右:球体モデルを用いて計算した同期間の粘弾性変形による重力変化.

5. 今後の展望

今後, データ解析の面では, 重力と地表変位の観測データを組み合わせることで, 断層すべり分布と粘性の同時推定をより精度よく行う手法の開発, 理論面では, 非線形な応力―歪関係, 地形, 粘弾性構造の３次元不均質等を考慮したモデルの開発が求められている. 粘弾性変形による地下の応力変化を見積もることは, 余震のトリガーの可能性を評価する上でも重要な課題である.

参考文献

http://www.eri.u-tokyo.ac.jp/okubo/ResearchHP/HP16.Viscoelasticity.pdf
Turcotte, D. L. and G. Schubert, Geodynamics, second edition, Cambridge University Press, Cambridge, England, 2002, 456 pp. (Chapter 7)
Karato, S., 2003. The Dynamic Structure of the Deep Earth, An Interdisciplinary Approach, 264 pp., Princeton Univ. Press, NJ.
Peltier, W. R., 1998. Postglacial variations in the level of the sea: implications for climate dynamics and solid-Earth geophysics, Rev. Geophys., 36, 603-689.
Sella, G. F., S. Stein, T. H. Dixon, M. Craymer, T. S. James, S. Mazzotti, and R. K. Dokka, 2007. Observation of glacial isostatic adjustment in ‘‘stable’’ North America with GPS, Geophys. Res. Lett., 34, L02306, doi:10.1029/2006GL027081.
Thatcher, W., and J. B. Rundle, 1979. A model for the earthquake cycle in underthrust zones, J. Geophys. Res., 84(B10), 5540–5556, doi:10.1029/JB084iB10p05540.
深畑幸俊 (2009): 線形粘弾性問題の時間無限大の解, 応用数理, 19, No.2, 84-96.
田中愛幸, 巨大地震による長期的な地殻変動及び重力場変動を球体地球モデルを用いて正確に見積もるための理論計算手法について, 測地学会誌, 59, 1-10, 2013.
Suito, H. & Hirahara, K., 1999. Simulation of postseismic deformations caused by the 1896 Riku-u earthquake, northeast Japan: Re-evalution of the viscosity in the upper mantle, Geophys. Res. Lett., 26, 2561–2564.
Tanaka, Y., Okuno, J.&Okubo, S., 2007. A new method for the computation of global viscoelastic post-seismic deformation in a realistic earth model (II)—horizontal displacement, Geophys. J. Int., 170, 1031–1052.
Tanaka, Y., V. Klemann, Z. Martinec and R. E. M. Riva, 2011. Spectral-finite element approach to viscoelastic relaxation in a spherical compressible Earth: application to GIA modelling, Geophys. J. Int., 184, 220-234.
Tanaka, Y., T. Hasegawa, H. Tsuruoka, V. Klemann and Z. Martinec, 2014. Spectral-finite element approach to viscoelastic relaxation in a spherical compressible Earth: application to the gravity field variations due to the 2004 Sumatra-Andaman earthquake, Geophys. J. Int., submitted.