重力測定と小型絶対重力計の開発
東京大学地震研究所 新谷昌人
1. 地球重力場の計測
1-1. 地上における重力測定
地上における重力 (重力加速度) は, 地球構成物質による万有引力 (引力) , 地球の自転による遠心力, 月や太陽から受ける潮汐力などの影響を受けている. そのため, 精密に重力を測定することによって, 地下や大気を含む地球全体の密度の分布, 物質の移動, 地球の回転変動などを調べることができる. 地球は自転運動による遠心力により, 赤道方向に約$1/300$の比率で膨らんだ回転楕円体に近い形状をしており, 引力と遠心力により地上における重力値は赤道 (約$978Gal$) に比べ北極や南極 (約$983Gal$) が$0.5%$程度大きく緯度による違いがある. また, 測定場所の標高h[km]によっておよそ$-0.3h[Gal]$の違いがある (たとえば富士山頂では麓より約$1Gal$小さい重力値) ことを考えると, 地上における重力は$980Gal$を中心に数Galの範囲ということになる. 測地学テキストにあるように, 地下密度の違いによる重力異常はその範囲の$1/1000$である数$mGal$の大きさである. このような空間的な違いや時間変動する重力場として月や太陽の引力に伴う潮汐効果がさらにその$1/10$の数百$\mu Gal$, 地殻変動や地下水移動, 火山活動に伴うマグマ等質量移動の効果は数$\mu$~数十$\mu Gal$, あるいはそれ以下である. このように, 空間的な違いの部分や時間変動成分を含め, 地上における重力測定の範囲としては, 1000Galから1$\mu Gal$までの9桁の範囲に及ぶ. そのため, 基準からのずれのみを測定する相対重力計と, 10桁以上の精度が得られる量子標準を用いた高精度の絶対重力計を使い分け, 空間的・時間的に広範囲に重力測定が行われている.
1-2. 人工衛星による重力測定
一方, 地球周回の人工衛星を用いた重力場の測定により, 地球全体の重力場の様子が詳しく調べられるようになった. 地下密度による引力によって生じる人工衛星軌道の乱れから逆に地下の密度構造が求められる. 別章に説明されているように, 地球規模の現象がとらえられており, 例えば, 地下の密度分布は大陸と海洋のパターンとはやや異なっていること, 季節により地球全体で水の移動が起こり重力変化している様子, 大地震の発生に伴って断層周辺の重力場が変化すること, 経年的な氷河の消失に伴う重力変化, 海面高度データと重力補正を組み合わて求められた海洋の大規模な流れなどが明らかになっている. ただし, 人工衛星による重力場測定は衛星がその地域の上空に来たときの情報となるため, 特定の地域の急速な変動を連続的に測定することはできない. また, 衛星軌道高度だけ離れた上空から測定となるため, それより小さいスケールの現象を捉えることは困難である. そのため, 観測対象の時間・空間スケールに応じて, 人工衛星による測定と地上の測定が相補的に用いられる.
本章では, 地上における重力測定と小型絶対重力計の開発について述べる.
2. 重力の相対測定と絶対測定
1-1. 重力の計測範囲
上述のように地上における重力測定は1μGalから1000Galまでの9桁に及ぶ. 地球の形状と遠心力による効果は数字の3桁目, 地下構造や地形の効果は5~6桁目以降, 潮汐その他の要因による時間変動する部分は7桁目以降である. つまり, 地球重力場は0.1%程度 (3~4桁) の計測精度では既知の値で一定であり, 地球科学的に意味のある計測をしようとする場合は5桁目以上を測定できる精度が必要である. これはたとえば, 1kgの質量に加わる力を10mg重より良い精度で計測することに相当し, あまり簡単なことではない. そこで, おもに2つの方法で重力測定が行われている. 相対重力測定と絶対重力測定である.
1-2. 相対重力測定
相対重力測定は, 簡単にいうとたとえば1kgの質量に加わる力の大部分をなんらか方法で釣り合わせて, そこからのずれの分だけを測定する方法である. 1kgのうち999gが釣り合っていれば, 残りの1g重の部分は1%の精度の測定で10mg重を測定できる. この場合, いかに安定に釣り合わせるかが問題となるが, 装置全体は小型で持ち運べる程度の大きさ・重量にできるため, 重力がわかっている基準点と測りたい観測点の間で相対重力計を持ち運んでそれぞれ測定し, 両者の測定値に基準点の重力値を加えて観測点の重力値を得ることができる. ある観測点に相対重力計を置いて連続測定を行い, 重力値の変動の観測や地震計のように地面の揺れによる加速度の観測で用いられることもある.
測地学テキストにあるように, ばねの伸びの変化$ds$から重力値変化$dg$を$dg=(k/m)ds$の関係から測定することが基本となるが, ばね定数$k$の変化$dk$も考慮すると$mg=ks$の関係から, $dg=(k/m)ds+(s/m)dk$ より, $dg/g=ds/s+dk/k$となり, $dk/k$により計測精度が決まることがわかる. 通常の金属のばね材では, $dk/k$は$10^{-4}/K$程度であり, $1mK (=0.001K)$ まで温度を安定させても, $dg/g=10^{-7}$であり, 潮汐による時間変動がやっと見える程度の精度にしかならない. そのため実際の相対重力計では, 装置の温度安定とともに温度係数の小さい特殊なばね材を用い, さらに温度係数がほぼゼロとなる温度付近で使うなどの工夫をして9桁に近い精度が出せるようになっている. しかし, 観測時以外にも温度保持のため常時保温ヒーターを駆動する必要があり管理が煩雑なこと, 振動により不連続 (テア) が生じる可能性があること, ばねの経年的な伸びが避けられないこと, あくまで相対値の計測であり基準点が必要, という計測上の欠点がある.
1-3. 絶対重力測定
一方, 基準点の重力値は正確に測定する必要があり, 絶対重力計が用いられる. かつては振り子の固有周期を測定し重力の絶対値が計測されていたが, 精度が6桁程度であった. 長さ$L$の振り子の固有周期Tは重力加速度$g$を用いて$T=2\pi\sqrt{L/g}$で表されるので, たとえば, 周期1秒の振り子 (長さ~$25cm$) が1000回振動する時間を1ミリ秒の精度で測定すれば6桁程度の精度でTが求められる. ただし, 同じ精度で$g$を求めるには振り子の長さも6桁程度で決める必要があり, これは$1m$の長さを1ミクロン$(1\mu m)$程度で測定することに相当する. また, 振り子を振らせている間に支点の部分がその精度でずれないように保持しなければならない. これらの誤差要因のため, 物理的な振り子を用いて6桁を超える精度で重力の絶対値を測定することは困難であった.
重力は質量に力を及ぼすから, 束縛力を与えなければその物体は力学法則で与えられる加速度運動をする. そこで, 空気抵抗の無い真空容器中で物体 (落体) を自由落下させた際の加速度運動を正確に測定すれば, その場所での重力の絶対値が測定できる. この方法は, 加速度運動を計測するためにレーザーの波長を基準とした距離計測法を直接用いることができ, 正確な原子時計と併せて計測すれば9桁以上の精度で加速度測定が可能である. また, 距離測定にレーザー光を用いるため, 物理振り子のような長さの計測誤差やその変化に相当する要因が無い. 近年では, 物体ではなく原子を自由落下させ, 原子干渉という方法で絶対重力を測定する方法も研究されている. 物体の形状や物性などの不確定さに伴う誤差や落体の消耗に伴う交換, 落下装置から生じる機械振動などの問題が無くなるメリットが大きい. この場合もレーザーが原子干渉の計測に用いられる. いずれの方式も, 地表の基準点に対する落体あるいは原子の運動を計測する原理であり, 基準点の地面振動加速度が計測誤差となることから, 基準点となる鏡は除振装置上に配置されている. 自由落下式の絶対重力計は, 波長安定化レーザー, 原子時計, 真空容器, 落下機構, 除振装置, データ解析システムなど, 正確な計測に必要な道具立てが多く, 相対重力計のような移動測定は簡単ではない. 実際には, 基準点の連続計測と観測点の計測にはそれぞれ絶対重力計と相対重力計を使い分けて使用されている. 以下では, 地震研究所で行われている小型絶対重力計 (TAG-1) の開発を例に挙げて, 絶対重力計で問題となる誤差や装置の応用範囲について紹介する.
3. 小型絶対重力計の開発
3-1. 絶対重力計の構成要素
絶対重力計は図1に示すように自由落下する落体 (Free-fall mirror) と除振された参照鏡 (Reference mirror) にレーザー (Laser) の光を照射し干渉光強度を検出器 (Detector) で電気信号に変換する. 落体がレーザー光の半波長動くたびに干渉光強度が明滅し, 原子時計の発する正確な時計の刻みで信号を記録する. 重力加速度 (単位:$m/s^2$) を9桁の精度で測定するには, 長さと時間についてともに9桁以上の精度が必要である. レーザーはヨウ素など既知のガス吸収スペクトルで波長を安定化したものが用いられ, その精度は9~10桁である. 原子時計はルビジウムあるいはセシウムなどの吸収スペクトルに同期した発振器であり, 11桁以上の精度がある. 長さ・時間とも原子や分子の吸収スペクトルを基準とした量子標準を用いて, 落体の加速度を9桁の絶対値で測定する. 小型絶対重力計 (TAG-1) の構成は, 図2のように落体と落下装置は真空容器 (Vacuum chamber) に収納され, 参照鏡が組み込まれた除振装置からの地面振動信号 (Seismic signal) も検出信号とともに収録 (Data acquisition) される. レーザー光源はヨウ素のスペクトルで安定化されたヘリウム・ネオンレーザー (赤色光) を基準に別のレーザーを同期安定化させたオフセット・ロック型のヘリウム・ネオンレーザーを用いている. ヨウ素安定化で用いられる変調の影響を避け, 強度の大きい出力が得られるメリットがある.
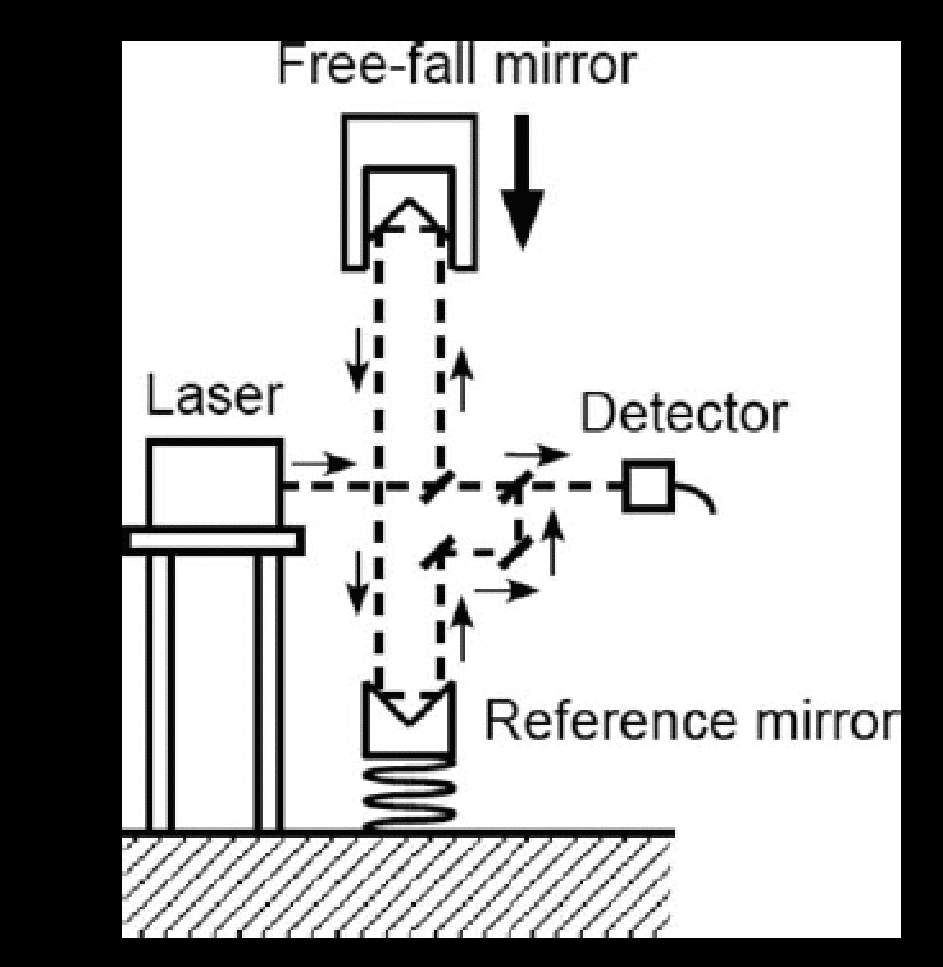
図1. 絶対重力計の構成要素
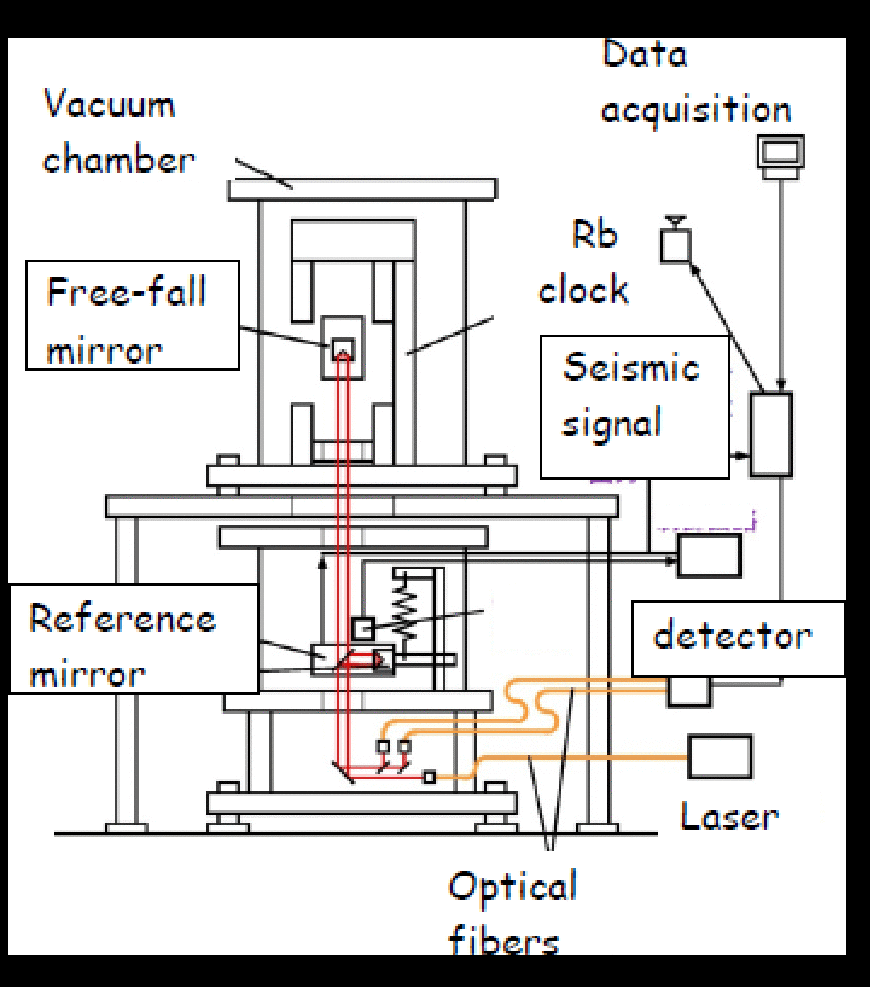
図2. 小型絶対重力計 (TAG-1) の構成
TAG-1では, 5分に1回の頻度で落体を落とし重力値を測定する. 干渉計は図3左, 同右下のように落体の変位に対してSin, Cosに対応する2位相の干渉縞を生成するように半波長板 (HWP) や1/4波長板 (QWP) が組み込まれており, 各信号によるリサージュ (図3右上) の位相角から落体の変位が求められる. 自由落下する落体の変位は時間に対して2次関数で変化するため, 計測された変位を2次関数でフィッティングした2次の係数から重力値が求められる. ただし, これには参照鏡の地面振動加速度が含まれているため, 参照鏡が組み込まれている除振装置からの地面振動信号を利用して補正し, 本来の重力加速度が求められる (図4) . 図5はTAG-1を用いて地震研究所霧島観測所 (宮崎県えびの市) で観測されたデータである. 干渉縞から求められた重力値を地面振動データ (seismic acceleration) で補正した結果が重力データ (gravity) である. 潮汐の理論値 (theoretical tides) とほぼ同じ重力変動が観測されていることがわかる.
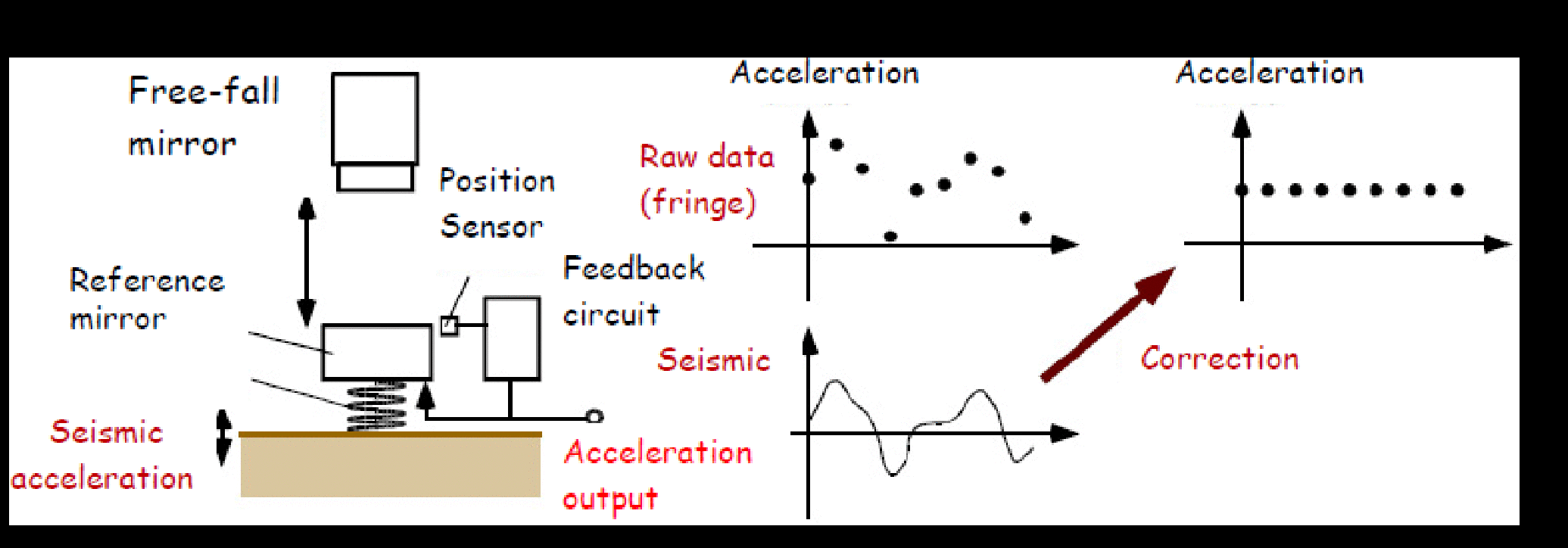
図3. TAG-1の干渉計とその信号

図4. 除振装置から得られた地面振動信号による重力計測値の補正

図5. TAG-1で測定された霧島観測所における絶対重力値 (gravity:左軸)
3-2. 測定誤差
絶対重力計で9桁の精度で正しい重力値を得るためには誤差を取り除くなどいくつかの補正をする必要がある. 偶然的 (ランダム) な誤差と系統的 (一定) な誤差に分けて考える.
偶然的な誤差として大きいものは地面振動である. 上述のように, TAG-1では地面振動信号を別に取得し補正している. 図5より霧島観測所では地面振動加速度は数百μGalであり, 補正によりその影響を数百分の1にできれば1μGalの測定精度が得られる. 補正が不十分でも偶然誤差であるので多数の測定データを平均すれば目標精度に達することができる. 参照鏡を長周期の除振装置 (Super spring等) に組み込み影響を取り除く方法もある. 干渉計の計測信号の読み取り誤差については, データを高速に取得したり, 落下時間を長くしたりして, 計測データ量を増やし平均化して低減させることができる. 落体の回転運動も誤差となる. 落体には入射光を並行に反射するコーナーリフレクタが組み込まれており, 落体の重心とリフレクタの光学中心 (光心) が一致するように調整されている. しかし, 両者の位置にhの高さ方向のずれがあると, 落下中の落体の回転角速度ωによりhω2の誤差が生じる. ωの2次で効くため, ωがランダムであっても重力値としては系統誤差になる. hは精密な調整を行えば10μm程度にできる. 1μGal以下の誤差にするにはωは30mrad/s以下にする必要がある. TAG-1では落下時に落体を素早く離すことで回転運動を生じにくくしている.
系統誤差は既知のものであれば計算により測定値を補正することができる. 装置内の落体の位置は重力測定する基準の高さ (たとえば床面) と一致していないため, その差を補正する必要がある (器械高補正) . 重力の鉛直勾配は0.3mGal/m程度であるが, 場所によって異なるため, 相対重力計で測定地点の重力勾配を実測して補正することが多い. 補正量が大きいと重力勾配の誤差の影響が無視できなくなる. そのため, 落体が上部に位置する絶対重力計では, 基準の高さを床面ではなく床から130cmの高さなどに設定している. 器械高は落下開始点と着地点との間にあるが, 干渉縞のデータ処理方法によってその位置関係は異なる. 重力で観測される潮汐は, 月や太陽の引力による重力加速度に地球の変形に伴う効果が加わったものであり, 月・太陽の位置関係と地球の内部構造により理論的に計算できるが, 仮定するモデルにより若干の違いが生じる (固体潮汐) . 海岸に近い地域ではさらに海洋の引力と加重による陸の変形の効果が加わる (海洋潮汐) . 潮汐の研究をする場合以外は理論値を用いて観測値を補正する. 計測高と潮汐の補正はともに数百μGalである. うち海洋潮汐補正は数~数十μGal以下であり, 海岸に近いほど補正量は大きくなる.
干渉計で用いられるレーザー光はほぼ平行ビームとなるように調整される. しかし, ビーム径が細いと回折のため球面的な波面になり, その位相が平面波の場合からわずかにずれ, 干渉計測の系統誤差が生じる. 1μGal以下の誤差にするためには, ヘリウム・ネオンレーザーの場合はビーム径はおおよそ5mm以上にする必要がある. TAG-1ではビーム径を測定し, 計算で補正している. 落体は移動しながらレーザー光を反射するため, 落下開始時と着地時で反射位置が異なりその間の光の伝播時間を考慮して落体の運動を求める必要がある. しかし, 計算が煩雑なため光の伝播時間の効果はそれを考慮しない計算からの補正量として通常扱う. 落体の落下時間や反射する方向 (前進か後退か) で補正量と符合が異なり, TAG-1の場合約10μGalのマイナスの補正量である. 真空容器内の残留ガスによる影響も系統誤差となる. TAG-1では実験的に求められた係数1.2Gal/Torrと観測中の真空度から補正を行っている. 干渉縞の計測で使用される光検出器や記録装置の周波数特性も誤差要因になる. ヘリウム・ネオンレーザーの波長で10cm程度の落下の場合, 干渉信号の周波数は0~4.4MHz程度まで変化する. その間の検出系の周波数特性による位相変化は系統誤差になる. それを避けるために, 干渉信号の最大周波数よりも十分速い検出系を用いることが望ましい. 大気による重力効果は, 観測地点の標高によって決まる標準的な大気圧と観測時の気圧から補正係数 (-0.3μGal/hPa) を乗じて計算し適用する. 極運動の補正は, 地球の自転軸のゆらぎにともなう遠心力の変動の補正で, IERS (International Earth Rotation and Reference Systems Service, 国際地球回転・基準系事業) で公表されている極運動座標から補正量を計算する. 数μGalの補正量である.
TAG-1 (図6) を用いた霧島観測所における観測で適用した系統誤差補正の値を表1に示す (A. Araya et al., Proc. of IAG Symposium on Terrestrial Gravimetry, TGSMM-2013, 98-104 (2014)) .
表1. TAG-1を用いた霧島観測所観測で適用した系統誤差補正の値

3-3. 小型絶対重力計の応用範囲
絶対重力測定は, 基準点を参照せずに単独で値が決められ, 相対重力測定におけるドリフトなどの不確定部分が無いという利点がある. 安定した基準点が確保できない火山島や地殻変動発生域では不可欠の重力測定法である. また, 同一地点での単独長期連続観測は相対重力計ではドリフトがあり困難である. 絶対重力計の小型化・低コスト化により, 従来アクセス困難であった火山体などさまざまな場所で絶対重力測定が展開できれば, 重力場の空間分解能や観測精度の向上が見込まれる. 例えば, 火山を取り囲む多数の観測点による面的重力場測定によるマグマ等地下流体の移動の検知や, 火山噴火・地震等の被災リスクが高く従来観測できなかった場所での連続観測も可能となるであろう.

図6. 小型絶対重力計TAG-1

