GOCEがもたらしたもの
京都大学大学院理学研究科 福田洋一
1. GOCEミッション概要
2009年3月17日に打ち上げられたGOCE (Gravity field and steady-state Ocean Circulation Explorer) 衛星は, 当初の予定を1年以上延長し, 長期にわたり地球の重力場を測定した後, 2013年10月21日にミッションを終了, その後, 11月11日に大気圏に再突入し終焉を迎えた. 21世紀に入り, 2000年7月15日にCHAMP(CHAllenging Minisatellite Payload)が, 2002年3月17日にはGRACE (Gravity Recovery and Climate Experiment)が打ち上げられ, 衛星による地球重力場観測の時代が到来したが, そんな中, GOCEは何度かの遅延を経て, 2000年代の最後になってようやくその実現に漕ぎ着けた.
GOCEの目的は, 短波長での静的な重力場の改良, すなわち, 高空間分解能で高精度に地球の重力場を測定しようとするもので, この点, 重力場の時間的変化の測定を狙ったGRACEとは, その目的がかなり異なっている. 具体的にGOCEが目指したものは, 空間分解能100kmで, 重力異常にして1mgal, ジオイド高にして1cmの精度であり, 海域では, GOCEの名が示す通り, 衛星高度計との組み合わせによる力学的海面高度の研究, また, 陸上では, 高精度なジオイド決定によるグローバルな高さ基準の統一などに貢献すると期待されている. さらに, 従来, 地上, 海上, あるいは航空重力測定では困難であった波長100kmより長波長領域での重力異常の精度向上により, 大陸の地殻構造, 地球内部の密度構造の研究など, 固体地球物理学への寄与も期待される.
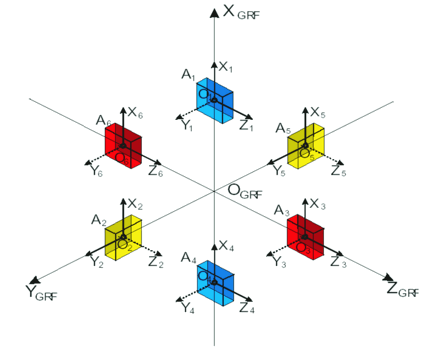
GOCEによる地球重力場の測定には, 高高度のGNSS (Global Navigation Satellite System) 衛星から低軌道のLEO(Low Earth Orbiter)衛星の軌道追跡を行うH-L SST (High-Low Satellite to Satellite Tracking)と重力偏差計(Gradiometer)を組み合わせた方法が用いられている. GOCEの重力偏差計は直交する3軸に加速度計を2組ずつ6台配置したもので(図1), これら18個の加速度計から得られる測定値を組み合わせることにより, 重力ポテンシャルV の6個の2階微分成分, Vxx , Vyy , Vzz , Vxy , Vxz , Vyz のすべてが計測される. 地球の重力場データは, H-L SSTにより計測される重力場の長波長成分に, 重力偏差計で測定される重力場の短波長成分を加えることにより得られる.
ところで, 短波長の重力場測定にとって重要な点は, 衛星の高度を出来るだけ低くすることである. 衛星の高度が下がると残留大気の影響が大きくなり, 継続的な飛行そのものが困難になるが, GOCEの軌道高度は当初260kmに設定され, ミッションの終盤では段階的に224kmにまで下げられた. このような超低高度での衛星観測は歴史上初めてであるが, それを可能にしたのは, 「宇宙のフェラーリ」の異名を持つ流線型でひれを持ったGOCEの形状(図2)や, 高性能なイオンエンジンとそれを用いたドラッグフリーシステムなどで, GOCEには, 衛星工学的にも数々の新技術が投入された.
2. GOCEによる重力場測定
地球上で測定される重力は, 地球の引力と自転による遠心力の合力である. ところで衛星では, 自転による遠心力は作用しないので, 地球の引力の効果だけが測定される. 地球の引力ポテンシャルVは, もし地球内部の質量分布が既知であれば, ニュートンの万有引力の法則に従って, それを地球全体で積分すれば計算でき, 緯度φ, 経度λ, 衛星の高度hとして,
\[V(\phi,\lambda,h)=\frac{GM}{a+h}\sum_{l=0}^{\infty}\sum_{m=0}^{l}\bigl(\frac{a}{a+h}\bigr)^{l} P_{lm}(\sin\phi)(C_{lm}\cos(m\lambda)+S_{lm}(\sin(m\lambda)))\tag{1}\]
と書くことができる. ここで$GM$は地心引力定数, $a$は地球の平均半径, $P_{lm}$は次数$l$, 位数$m$のルジャンドル陪関数, $C_{lm}$, $S_{lm}$は地球内部の質量分布によって決まる係数で, Stokes係数と呼ばれる. (1)式で, 地球重力場を決めるということは, Stokes係数を決めることであり、短波長まで精度良く決めるということは, 高い次数$l$のStokes係数まで正確に決めるということである.
(1)式から, 次数$l$の重力場信号は, 衛星の高度hに対して $\displaystyle\frac{a}{a+h}$ の$l$乗で減衰し, 高次の信号の減衰が如何に大きいかがわかる. 図3は, 横軸に次数$l$, 縦軸に対数目盛をとり, 高度180km, 250km, 400km, 600kmで, 地表での重力ポテンシャルに対する次数$l$での重力場の減衰を描いたものである. この図の次数$l=250$付近で比べると, ほぼGRACEの高度である約400kmに対して, GOCEの250kmでは2桁以上感度が高く, もしGOCEの高度を180kmまで下げることができれば, さらに1桁程度の向上が見込まれることが判る. 重力場測定にとって衛星の高度が低いことは大変有利なのである.
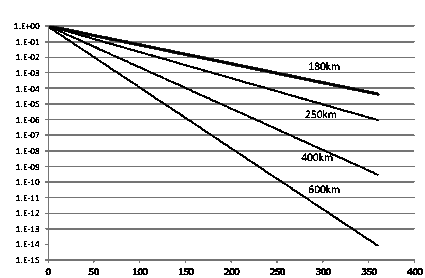
図3. 衛星高度による重力ポテンシャルの減衰. 横軸に球面調和関数の次数, 縦軸に地表での重力ポテンシャルに対する相対的な信号の強さを示す. 図中の数値は衛星の高度.
3. GOCEによる地球重力場モデル
GOCEによる測定データは, 基本的にはH-L SSTによる軌道追跡データと, 重力偏差計による重力ポテンシャル$V$ の2階微分成分であり, これらの衛星軌道上でのデータは, 感度の補正や座標回転など必要な補正が施された後, Level-2データとして公開されている. さらに, これらのデータを基に, 上述のStokes係数が計算され, 複数のEGM (Earth Gravity Model)が利用に供されている. GOCEのEGMとしては, 重力場の計算方法の違いから, DIR (Direct Solution), TIM (Time Wise Solution), SPW (Space Wise Solution)の3種類のモデルがあり, それぞれ公開時期の違いから, R(Release)1〜R5 (SPWはR4まで)のバージョンが公開されている. それぞれのモデルの特徴として, TIMではGOCE以外のデータは一切用いていないのに対し, DIRでは先験情報としてGRACEのデータなども利用していること, またSPWでは, 既存の重力場モデルEGM2008などを通じ, 間接的に地上データの情報も含まれることが挙げられる.
GOCEミッションの最後の1年間には,軌道高度を段階的に下げたデータが得られているが,現在,これらのデータをすべて用いたEGMとして,DIR-R5では300次,また,TIM-R5では280次までの係数が公開されている. また, 例えばGOCOモデルのようにGOCEのデータだけでなく低次の係数での精度が高いGRACEのデータやSLRなど他のデータと組み合わせたモデルの開発も進んでおり, 今後, このような新しいモデルも公開されていくものと期待できる. 一方, 少なくとも今後10年程度は, 超低高度での重力場測定衛星の計画はなく, 地表データを含まない衛星データだけによる地球重力場モデルとしては, 当分の間, GOCEを超えるデータの出現は期待できない. その意味でも, 地球重力場モデルの改良に果たすGOCEの役割は極めて大きいと言える.
4. 力学的海面高度と海流
GOCE (Gravity field and steady-state Ocean Circulation Explorer)の名前の由来を理解するには, 海面高度計の説明が必要である.
海面高度計とは, マイクロ波レーダーを用い, 衛星軌道から海面までの距離を測定するもので, 衛星の軌道が正確に判っているとすると, 地球楕円体から海面までの距離, すなわち海面高が測定される(WEB版測地学テキスト2-4-1-5. 図13参照). もし, 海面が理想的に静止しているとすると, それは一つの等重力ポテンシャル面となるはずで, これがジオイドである. しかし, 実際の海面は様々な原因で常に変動しており, 特に海流が存在する場合には, 図4に示すように, 海流(地衡流)によるコリオリ力と海面の傾斜による圧力傾度力が釣り合うように海面に起伏が生じる. このようなジオイドに対する海面の起伏は力学的海面高度と呼ばれ, 逆に, 力学的海面高度が判れば, 地衡流の仮定から海流の流速や流量を知ることができる.
海面高の測定精度は, 1990年代以降のTOPEX/PoseidonやJason-1/2では, すでに2〜3cmに達しており, 海洋変動やその他, 多岐にわたる海洋学的な応用研究に用いられている(例えば、福田, 2000). 一方, 海域での重力測定は, 特殊な観測船によるごく限られたものだけであり, 重力測定データを用いたジオイドの精度が劣っていたため, 力学的海面高度を正確に決めることができず, 1980年代後半より, 衛星による重力場測定の早期実現が望まれていた. GOCEの名はこのような歴史的背景に由来したものである.
GOCEの初期わずか2ヵ月間のデータだけによるEGM(DIR-R1)と海面高度計のデータを用い, 力学的海面高度や海流を推定する検証研究がなされているが(Knudsen et al., 2011), その結果は, これまでの衛星データだけを用いたどの結果よりも良いものであった. 力学的海面高度の基準として, 一旦, 高精度なジオイドが得られれば, 過去に遡って海流の研究に用いることができる. GOCEのデータを用いたEGMは今後も改良版が公開されるはずであり, 今後, それら改良されたモデルと, 長年蓄積された衛星高度計データを用いることで, 力学的海面高度やそれに関連した海洋学的研究が大いに進むものと期待できる.
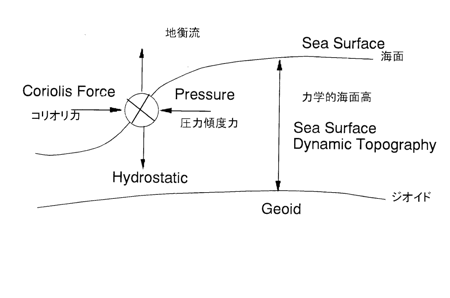
図4. 力学的海面高度と海流(地衡流)
5. グローバルな高さ基準の統一
海域での力学的海面高度はジオイド面から測った海面の高さであるが, 陸の高さの基準はどのよう決められているのだろうか. 我が国の測量法第11条では, 「平均海面からの高さで表示する」となっており, 具体的な値として, 測量法施行令に日本水準原点の原点数値は「東京湾平均海面上24.3900メートル」(平成23年10月21日改正)と定められている. すなわち, 高さの基準はローカルな平均海面であり, これは, 海面変動や力学的海面高度を無視した程度の近似でのジオイド面からの高さと考えることもできる. このような事情は我が国に限ったことではなく, 現在, 世界中のほとんどの国での高さはローカルな平均海面に準拠しており, このため, 相互に1m以上の違いが生じることも稀ではない. 一方, グローバルな位置座標については, ITRFによりmmオーダーでの精度が得られており, その精度との整合性や, また長期的な海面変動の監視の為にも, cm〜mmオーダーでのグローバルな高さの統一(WHS:World Height System Unification)が求められている.
統一されたWHSを実現するためには, 現在, 各国でばらばらな高さの基準面を, グローバルに高精度で決定されたジオイド面に移す必要がある. このためには, 長波長の重力モデルとして高精度なEGMが不可欠であり, GOCEデータに期待が寄せられる. WHSの実現でもう一つ重要なことは, ジオイド面と一致する高さ, すなわち理想的に静止した海面の位置を決めることである. ジオイド面は重力場の一つの等ポテンシャル面であるので, これはジオイド面のポテンシャルの値W0を決めることと同義である. ところで, 現実の海洋では力学的海面高度を無視することはできないので, 陸の高さ基準としてジオイド面を決めるためにも力学的海面高度を知る必要があるというのは面白いところである.
現在, WHSの実現に向けた取り組みが各国で進められているが, 例えば, カナダではCGVD2013(Canadian Geodetic Vertical Datum of 2013)として, 2013年11月に, 正式にジオイド基準の高さへの移行を決めており, W0の値として 62,636,856.0 m2/s2を採用している. また, 国境を接する米国でも2022年を目標にジオイド基準の高さへの移行に向けて準備中でW0としてCGVD2013と同じ値を採用することになっている.
ところで, GOCEのEGMによるジオイドの精度は空間波長100kmで1cm程度とされているが, それより短波長の領域では誤差が大きくなり, 空間波長10km程度では数10cm程度の誤差が予想される. このため, 短波長の領域では, 地表の重力場データが不可欠であり, 例えば米国では高さ基準の再構築に向け, GRAV-D (Gravity for the Redefinition of the American Vertical Datum)プロジェクトとして, 航空重力や地表での重力測定などデータの整備を進めている. WHSの統一に向けたこれら現実的な動きを加速させたという意味でも, GOCEの果たした役割は大変に大きい.