GNSS-TEC法でみる地震と火山噴火
北海道大学理学研究院 日置幸介
1. GNSS-TEC法について
衛星測位システム(Global Navigation Satellite System, GNSS)は, 複数の衛星が発射するマイクロ波を地上局で受信し, その搬送波位相の変化から高精度の測位を行うシステムである. 従来米国が打ち上げた全地球測位システム(Global Positioning System, GPS)が主に用いられてきたが, 昨今はロシアのGLONASS, 中国の北斗(Beidou), 欧州連合のGalileo等のグローバルなGNSSに加え, 日本の準天頂衛星システム(QZSS)などにも対応可能な受信機が主流となりつつある.
我が国では地殻変動の計測を目的とした稠密な連続観測網GEONET (GNSS Earth Observation Network) が国土地理院によって展開されている. GPSの場合, 搬送波は1.5 GHz ($L_1$)および1. 2 GHz ($L_2$) の二つの周波数が同時に用いられる. 電離圏と呼ばれる超高層大気では, 太陽放射によって大気分子・原子の一部が電離しており, 電子がマイクロ波の伝搬を遅延(電離圏遅延)させる. GPS受信機は, 二周波を同時受信することにより, 周波数の二乗に逆比例する電離圏遅延を除去しているのである. 他のGNSSでも, 周波数はやや異なるものの基本的に同じ原理を採用している. その時に用いられる$L_1$と$L_2$の線形結合(Ionospheric-free Combination, 以下の式では$L_3$と表現する)はそれぞれの搬送波周波数を$f_1$, $f_2$とすると,
\[ L_{3}=\frac{f_{1}^{2}}{f_{1}^{2}-f_{2}^{2}}L_{1} - \frac{f_{2}^{2}}{f_{1}^{2}-f_{2}^{2}}L_{2} \tag{1} \]
であらわされる. ここで$L_1$, $L_2$は, 観測された位相に波長を掛けて長さ(m)の単位にしている. 一方$L_1$と$L_2$の単純な差(ここでは$L_4$と呼ぶ)は, 電離圏の情報のみを含んでおり, 中性大気遅延や衛星位置, 局位置などの情報は差をとった時に除かれている. そのためGeometry-free Combination(幾何学的要素が含まれない線形結合)と呼ばれる.
\[ L_{4} = L_{1} - L_{2} \tag{2} \]
$L_4$は視線に沿って積分した電子の数に比例するため, 主に電離圏研究に用いられてきたが, 地震や火山噴火などの固体地球に関連した現象に起因する電離圏擾乱の研究も盛んになりつつある. ここでは, 測地学会誌に解説・入門講座として執筆した日置他(2010)をベースとし, GNSSの生データを用いて電離圏の様々な擾乱を観測する手法と, 最近の研究成果のいくつかについて解説する.
2. RINEXファイルからのTECの作成
GNSSデータの解析は, 衛星や局の位置, 地球回転, 潮汐, 中性大気遅延等の様々な要因をすべて考慮する必要があるため, 概して複雑で個人レベルでのプログラム作成は難しい. 一方$L_4$では, これらの要因のすべてが(2)式で差を取る時に取り除かれているため, データ解析は本質的に簡単である. そのため, 既存のGNSS解析ソフトウェアで$L_4$に相当する量を出力させて解析に用いることも可能だが, 共通フォーマット(Receiver Independent Exchange format, or RINEX format)のGNSS生データのファイルを直接読んで$L_4$の時系列を作るのが手っ取り早い.
筆者のウェブページ(http://www.ep.sci.hokudai.ac.jp/~heki/software.htm)で, GPS限定ではあるが, RINEXファイルを$L_4$に変換するフォートランプログラムrdrnx.fを公開している. そのプログラムでは, 最初にRINEXファイルのヘッダー(# / TYPES OF OBSERVの行)を読みこみ, 様々な種類のデータの順番を確認する. 例えばオンライン公開されているGEONETのRINEXデータには$L_1$/$L_2$の位相である “$L_1$, $L_2$”, Pコードを示す“P2”やC/Aコードの “C1”, また昨今は$L_1$/$L_2$の信号対雑音比を表す “S1/S2”なども含まれる. 次にデータ本体部分をエポック毎(GEONETでは30秒毎)に読み込み, 様々な衛星で得られた$L_1$と$L_2$の位相を取り出す. 位相にそれぞれの波長を掛けて単位をラジアンから長さに変換し, (2)式のような差をとって$L_4$を求め, 衛星毎にソートした時系列を出力する. このプログラムでは$L_4$ (単位m) に(3)式のように, 適当なファクターを掛けて, 視線方向の電子数を積分した全電子数Total Electron Content (TEC)に換算してある.
\[ \Delta TEC = \frac{1}{40.308}\frac{f_{1}^{2}f_{2}^{2}}{f_{1}^{2} - f_{2}^{2}} \Delta L_{4} \tag{3} \]
TECの単位はTECU (TEC unit, 1 TECUは視線に沿った底面積1 m2の円柱に1016 個の電子が含まれることを意味する) である. 日本列島では, 太陽静穏時の昼間のTECはおおむね10-20 TECU程度であり, 夜間は数TECUに下がる. 上記のページには入力ファイル(RINEX形式)と出力ファイルの見本も置いてある.
位相データには一般的に整数値の不確定性があるため, 実際には$L_4$の絶対値に意味はなく, 衛星の観測開始から終了までの時間変化にのみ意味がある. (3)式で$\Delta$$L_4$および$\Delta$$TEC$となっているのはそのためである. RINEXファイルに二周波のコード情報(C1/P1およびP2)が含まれている場合は, それらの差に$L_4$を合わせることによって整数値不確定性を除去することができる. さらにそこから, 受信機の周波数間バイアスと衛星の周波数間バイアスを除去すれば正しいTECが得られる. これらの周波数間バイアスは電子航法研究所からウェブで公開されている(http://www.enri.go.jp/~sakai/pro.htm)(坂井, 2005).
図1a-eは, こうして得られた茨城県鹿嶋のGNSS点(93009)での2011年3月11日のTEC変化を衛星毎に曲線で描いたものである. 図1a に示す疑似距離の差(ここではC1とP2の差)に, $L_4$を合せ込むことによって製数値不確定性を取り除いたものが図1bである. そこから受信機の周波数間バイアスを除去し(図1c), さらに衛星毎の周波数間バイアスを取り除いて得られた図1dが, バイアスの無い真の$L_4$である. U字型の変化が顕著であるが, これは主に昇って沈む衛星の仰角変化に伴って視線ベクトルが貫通する電離圏の厚さが変化するためである(斜めに視線が貫く場合のTECをSlant TECと呼ぶ). U字型の変化の大きい左側の部分が電子密度の高い昼間, 小さい部分が電子密度の低い夜間に相当する. 図1dに高度300 kmのF層への入射角の余弦をかけて鉛直方向のTEC(Vertical TEC)に直したものが図1eである. 見かけの変化が取り除かれて, 電子数の日周変化が直接見えるようになっている.
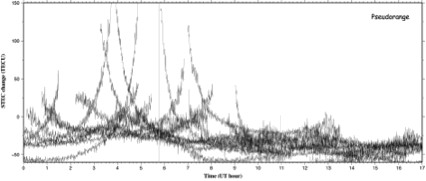
図1a GNSS局93009(茨城県鹿嶋市)における2011年3月11日の視線方向の全電子数(STEC)を疑似距離(コード)から求めたもの. コードは$L_1$がC/Aコード, $L_2$がPコードである. ノイズが多く, 細かい時間変化の議論には適さない. 縦の直線は東北沖地震の発生時刻を示し, それに伴う擾乱がb-eでは見えている.
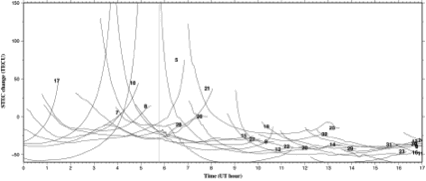
図1b 図1aと同じ日の搬送波位相から求めたSTECを, 図1aの疑似距離データにあわせることによって整数値バイアスを除去したもの. 周波数間バイアスが除去されていないため負の値も見られる.
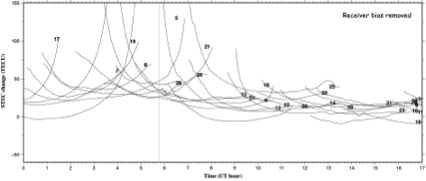
図1c 図1bのSTECデータから, この局の受信機固有の周波数間バイアスを除去したもの. 負の値はみられないようになった.
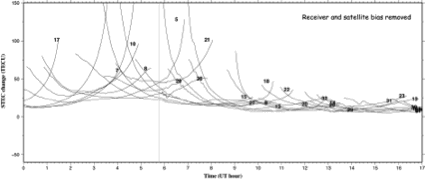
図1d 図1cからさらに衛星毎に異なる周波数間バイアスを除去したもの. これでようやく正しいSTECが求められたことになる.
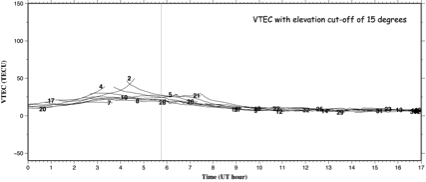
図1e 図1dのデータに視線が電離圏F層(高度 300 km)を貫く入射角の余弦をかけて鉛直TEC (VTEC) に換算したもの. 見かけの変化が消えて, 正午付近に最大を持つ日周変化が見えている.
3. 地震と火山噴火に伴うTECの振動
火山噴火に伴う電離圏擾乱は, ブルカノ型の爆発的噴火で発生した音波が熱圏に達してF領域の電離圏に電子密度の濃淡を生じさせたものである. Heki (2006) は2004年9月の浅間山噴火の際に生じた電離圏擾乱から火山爆発のエネルギーを推定している. その後Dautermann et al. (2009)は, 西インド諸島Montserrat島火山の2003年の爆発的噴火に関して同様の研究を行っている. また日置他(2010) には, 2009年十月に発生した桜島火山の爆発的噴火に伴うTEC変化の例が示されており, Peak-to-peakで最大0.2-0.3 TECU程度の擾乱が熱圏の音速で南に伝搬してゆく様子がわかる. 擾乱は音波が熱圏に達するのに要する10分程度経過してから現れ, しばしば2分弱の周期を持つ.
地震に伴う電離圏の擾乱(CID, Coseismic Ionospheric Disturbance)(e.g. Heki and Ping, 2005)には, 表面波(レーリー波)による地表の上下運動が作った音波が熱圏に達してもたらす擾乱と, 震源近くの地表の地殻上下変動が作った音波が直接熱圏に達して起こす擾乱の二種類がある(図2). 前者は表面波の伝搬速度(4 km/sec程度)で伝わるため, 大きな地震では熱圏での音速(1 km/sec以下)で伝わる後者と明瞭に区別できる(Astafyeva et al., 2009). 図3は, 2011年3月9日02:45UTに宮城沖で発生した, 東北沖地震の前震とされるMw7.3の地震がもたらした電離圏擾乱を示す. この擾乱は伝搬速度が比較的遅く, 表面波起源のものではなく直達音波による擾乱であることが分かる. 2011年東北沖地震では, 津波が励起した大気の内部重力波による同心円状の電離圏の擾乱が見られたことが報告されている(Tsugawa et al., 2011).
Heki et al. (2006) はスマトラ・アンダマン地震に伴う電離圏擾乱を解析して, 断層すべり量や破壊伝搬速度を拘束する試みを行っている. またCahyadi (2014) は, 20個を超える事例から地震の規模と地震時電離圏擾乱の振幅の経験則を確立し, 電離圏擾乱を観測することによって地震10分後にの地震のマグニチュードをある程度の精度で推定できることを示した. 直達音波による擾乱は距離に伴う幾何減衰が大きく, 図3に示した擾乱も震源から300 km程度で見えなくなっている. 擾乱の周期は約4.5分で火山噴火による擾乱に比べて長い. これは大気の共鳴周波数 (e.g. Nishida et al., 2000) の一つに一致している. 大きな地震では, しばしばこの周波数のTEC振動が30分から1時間の間継続する (Cahyadi, 2014).
地震, 火山噴火いずれの例でも擾乱の周期は十分短いため, 衛星の仰角や太陽天頂角の変化に伴う長周期の変化と混同する危険性は少ない. 図3の例では, 生の鉛直TEC変化をそのままプロットしている. また, 地震や火山噴火に伴う電離圏の擾乱が南に選択的に伝搬してゆくのは, 超高層での電子の動きが地磁気の方向に拘束されるため, 北向きの音波が選択的に減衰されることを反映している(Heki and Ping, 2005). この伝搬指向性は南半球では反転して北向きが卓越する. 以上に挙げた擾乱はいずれも地震や火山噴火の直後に生じるものであるが, Heki (2011)および Heki and Enomoto (2013)は, Mw8.5を超える巨大地震の約40分前から電離圏全電子数が前兆的な上昇を見せることを報告している. 図4に, 2010年チリ地震(マウレ地震, Mw8.8)での観測例を示す. 地震後の音波による擾乱(鋭い正のピーク)に加えて, 地震の約40分前にTECの正の異常が見えている.
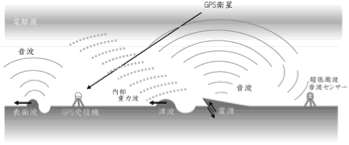
図2 地震や津波に伴って大気中に音波や内部重力波が励起され, それが電離圏に達して擾乱を発生させる(Heki et al., 2006). 音波の励起源には, 地震時地殻上下変動によるものと, 伝搬するレーリー波の両者があり, それぞれ特徴的な伝搬速度を持つ.
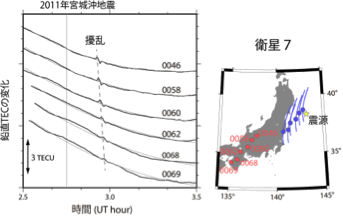
図3 2011年3月9日に宮城沖で生じたMw7.3の逆断層型地震(2011年東北沖地震の前震とされる地震)に伴う電離圏の擾乱. 左の図は鉛直TECの地震前後一時間の時系列で, 縦線で示す地震発生の約十分後に周期4分程度で正の初動(TEC増加で始まる)を持つ擾乱が顕著である. 擾乱は電離圏高度の音速で南に伝搬する. 右の図に, データを取得したGNSS局(赤丸)と, そこからGPS7番衛星を見た時に, 視線が高度300 kmの層を貫く点の軌跡(SIPの軌跡)を示す(青丸は擾乱発生時刻におけるSIPの位置).
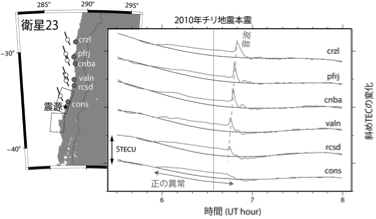
図4 2010年2月のチリ地震前後に23番のGPS衛星を観測して得られたTECの時系列. 地震約十分後の鋭い正のピークは, 地殻上下動に励起された音波が, 電離圏F領域に達して起こした擾乱である. それら地震後の擾乱に加えて, 地震の約40分前から正の異常が見える. 黒丸で示すGPS局からこの衛星を見ると, 黒い線はSIP軌跡で, 白丸が地震発生時のSIP位置である.
4. 視線ベクトルと電離圏の交点
$L_4$はgeometry-freeであり, 局位置や衛星位置などの幾何学的なことは「ほぼ」無視できるが, 例外的に幾何学的な計算が必要になる場合がある. それは, ある局で受信したあるGNSS衛星の電波から求めたTECが, 地理的にどのあたりの電離圏を見ているかを求める場合である. 実際の電離圏は上下に幅を持っているが, 便宜的に最も電子密度の高い高度(日本では300 km程)に薄い層を仮定し, 衛星と受信機を結ぶ視線ベクトルがその層と交わる点(IPP, Ionospheric Penetration Point), およびその地表への投影点(SIP, Sub-ionospheric Point)を求めて, 「緯度何度, 経度何度の電離圏を見ている」と表現することが多い.
既に紹介したウェブサイト(http://www.ep.sci.hokudai.ac.jp/~heki/software.htm)では, RINEX形式のGPS軌道情報ファイルを読み, そこに含まれているケプラー要素から, 諸衛星の地球固定系における位置を三分ごとに計算するプログラムrdeph.fが提供されている. そこから, 特定の時刻の衛星位置を内挿して求めれば, あとは局位置と衛星位置を結ぶベクトルが特定の高度の層を貫く点の座標を初等的な数学で計算することができる. 図2のSIPの座標はこのようにして求めたものである. なおSIPはその定義から本質的に高精度で求める必要がない. 様々な高度に分布した電子を高度300 kmで代表させた点ですでに大幅な近似だからである. 従って軌道精度も放送暦以上のものを追求する必要はない. なおGLONASS衛星の軌道情報はケプラー要素ではなく, 地球中心を原点とする三次元直交座標での位置と速度として与えられており, GPSとは異なるプログラムが必要となる.
5. GNSS-TEC法の可能性
ここでは主に地震や火山噴火に伴う電離圏変動をGNSS-TEC法で研究する事例を紹介したが, 固体地球以外にも様々な研究テーマが存在する. 中でも稠密GNSS網を利用した移動性電離圏擾乱(Traveling Ionospheric Disturbance)の観測は1990年代から盛んである. GEONETの稠密性を利用した観測対象としてスポラディックE層(Es)の二次元的なマッピングがある. Maeda and Heki (2014)は, いくつかのEsについて, それらが特徴的な東西に延びたパッチ状の分布をしていることを明らかにした. またロケットの排気に含まれる水分子と電離圏中のプラズマの化学反応によって電子の枯渇が生じる. Ozeki and Heki (2010)は, その現象を利用して北朝鮮が1998年と2009年に発射した弾道ミサイルであるテポドン1号と2号の軌道を追跡し, 排気量の推定を行った.
測地学の専門知識を持つ教員が所属する日本の大学では, GNSSを用いた研究を大学院の学位論文や学部の卒業研究のテーマとすることが多い. それらのテーマは, 最近発生した地震に伴う地殻変動に関する研究であったり, 地震間の地殻変動の解析から地下における断層固着部分を推定する研究であったりと多彩である. また大気遅延から可降水量を求めて, その時間変化と気象現象の関連を探るGNSS気象学的な分野にも様々な興味深い研究テーマがある. しかし, それらの研究を自分で作成した計算機プログラムによって行うことは困難であり, 既存のGNSSデータ解析ソフトウェアをブラックボックスとして利用することが多い.
$L_4$の解析は本質的に簡単で, 大学院生や卒論生が気軽にプログラムを作成してRINEXファイルからそれらの情報を抽出することができ, 努力に対する教育効果が高い. また本文中で紹介したプログラムを使用すれば, すぐに解析に取り組むこともできる. データの扱いが簡単であるにも関わらず, 本論文で紹介したように$L_4$の解析による研究対象はバラエティに富み, 未開拓の領域もまだ多いと考えられる. 今後は様々な大学や研究所でGNSS-TEC法による地球物理学研究が普及し, 新たな発展を見せることを願っている.

