4-8. 弾性論の基礎
高知大学自然科学系 田部井隆雄
神奈川県温泉地学研究所 里村幹夫
京都大学大学院理学研究科 福田洋一
4-8-1. 応力
物体内部に$x_1, x_2, x_3$をとる. $x_1$軸に垂直な微小面を考え, 面を通して働く力を単位面積あたり$p_{11}, p_{12}, p_{13}$とする(図1). このとき, 面に垂直な$p_{11}$ を法線応力, 面に平行な$p_{12}$ と$p_{13}$ を接線応力と呼ぶ. 応力の単位は圧力と同じPaであるが, barが用いられることもある.
\[ 1 [bar] = 10^{6} [dyn/cm^{2}] = 10^{5} [N/m^{2}] = 10^{5} [Pa] \tag{1} \]
物体中に各辺の長さが$dx_{i}$の微小体積を考える(図2). 力は応力と面積の積で与えられるので, 面EFGHを通して働く$x_1$方向の力は
\[ p_{11}dx_{2}dx_{3} \tag{2} \]
面ABCDを通して働く$x_1$方向の力は
\[ \left(p_{11} + \frac{\partial \rho_{11}}{\partial x_{1}} \right) dx_{2} dx_{3} \tag{3} \]
である. この微小体積の変形には, 力そのものではなく, 各部に働く力の差が寄与する. 従って, 変形を議論するには両者の差である
\[ \frac{\partial p_{11}}{\partial x_{1}}dx_{1}dx_{2}dx_{3} \tag{4} \]
が問題となる.
同様に, $x_1$方向には, 面ABFEを通して
\[ p_{21}dx_{1}dx_{3} \tag{5} \]
の力と, 面DCGHを通して
\[ \left( p_{21} + \frac{\partial p_{21}}{\partial x_{2}}dx_{2} \right)dx_{1}dx_{3} \tag{6} \]
の力が働く. 両者の差は
\[ \frac{\partial p_{21}}{\partial x_{2}}dx_{1}dx_{2}dx_{3} \tag{7} \]
である.
さらに, $x_1$方向には, 面BCGFを通して
\[ p_{31}dx_{1}dx_{2} \tag{8} \]
の力と, 面ADHEを通して
\[ \left( p_{31} + \frac{\partial p_{31}}{\partial x_{3}dx_3} \right)dx_{1}dx_{2} \tag{9} \]
の力が働く. 両者の差は
\[ \frac{\partial p_{31}}{\partial x_{3}}dx_{1}dx_{2}dx_{3} \tag{10} \]
である.
以上をまとめると, 微小体積の$x_1$方向の変形には
\[ \left( \frac{\partial p_{11}}{\partial x_{1}} + \frac{\partial p_{21}}{\partial x_{2}} + \frac{\partial p_{31}}{\partial x_{3}} \right)dx_{1}dx_{2}dx_{3} \tag{11} \]
が寄与する. $x_2, x_3$方向にも全く同じ議論が成り立つ.
微小体積の質量を$dm$ , 微小体積中の1点の変位を${\mathbf u}(u_1, u_2, u_3)$とすれば, 運動方程式は
\[ dm\frac{d^2 u_{i}}{dt^2} = \sum_{j}\frac{\partial p_{ij}}{\partial x_{j}}dx_{1}dx_{2}dx_{3} \tag{12} \]
となる. 一般に, ${\mathbf u}$の勾配は十分小さいので, 密度を$\rho$として
\[ \rho \frac{\partial^2 u_{i}}{\partial t^{2}} = \sum_{j} \frac{\partial p_{ij}}{\partial x_{j}} \tag{13} \]
が成り立つ.
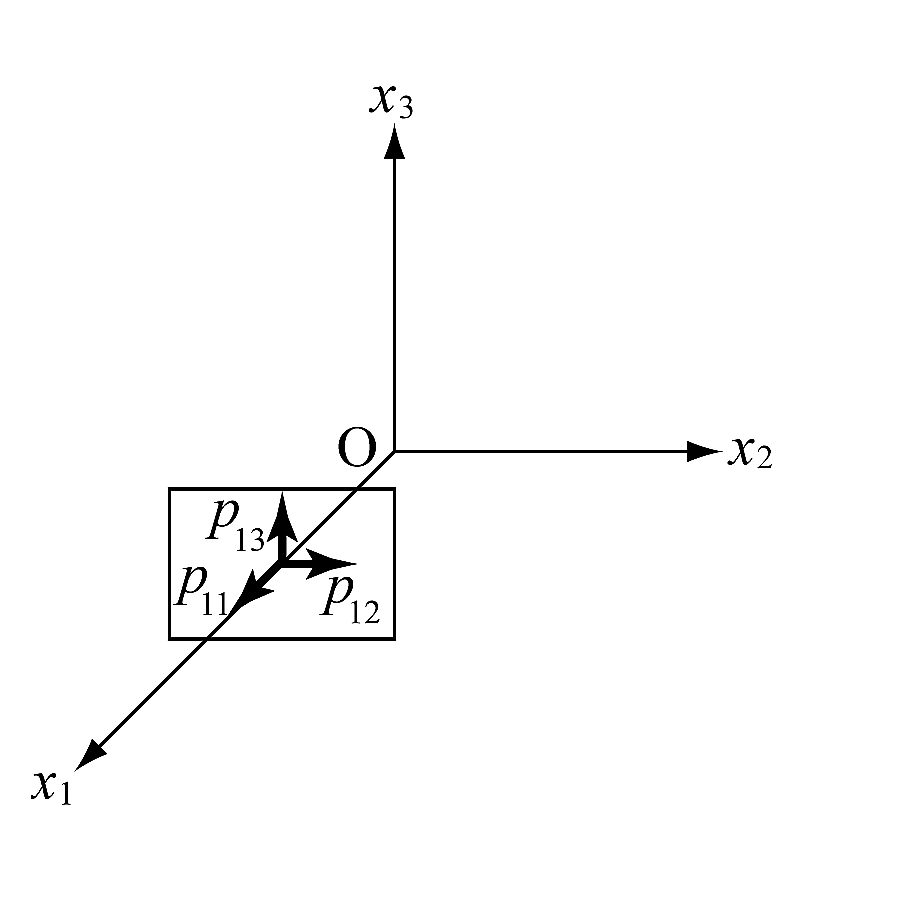
図1
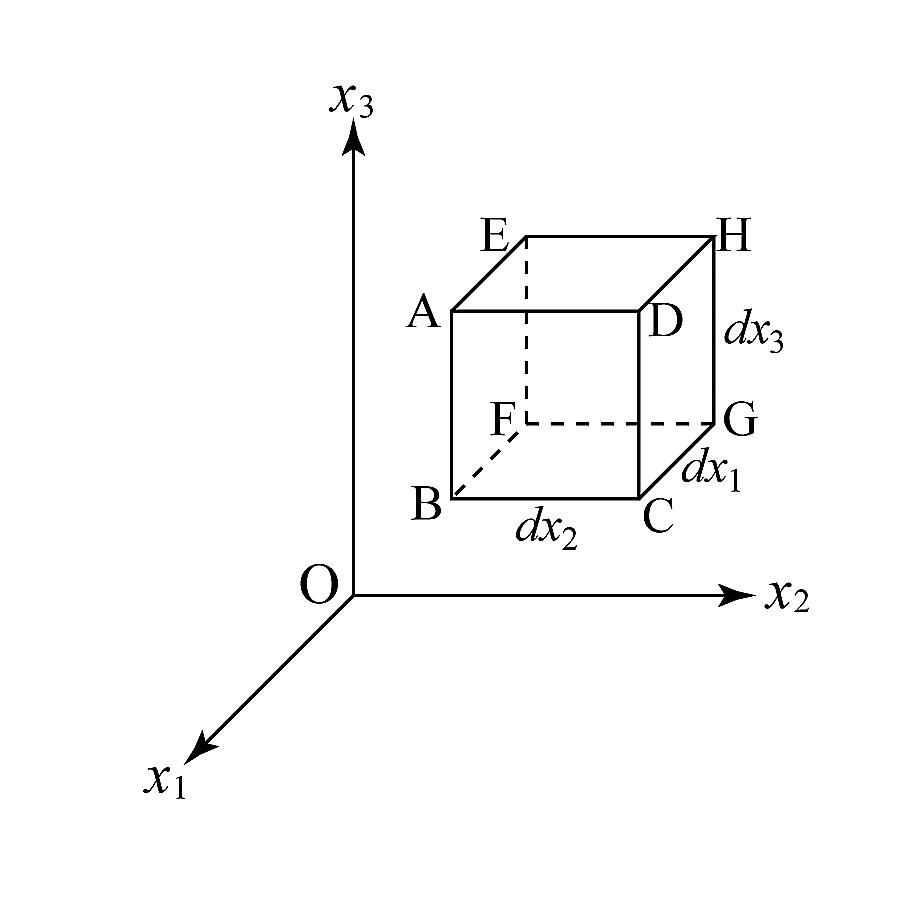
図2
4-8-2. ひずみ
物体内部に点$ P(x_{1}, x_{2}, x_{3}) $, その近傍に 点$P'(x_{1} + dx_{1}, x_{2} + dx_{2}, x_{3} + dx_{3})$をとる. 物体が変形したとき, 点P, P'の変位ベクトルをそれぞれ${\mathbf u} (u_{1} , u_{2} , u_{3})$, ${\mathbf u}' (u_{1} + du_{1} , u_{2} + du_{2} , u_{3} + du_{3})$とし, 変形後の位置をそれぞれQ, Q'とする(図3). ${\mathbf u}' - {\mathbf u} = (du_{1}, du_{2}, du_{3})$はPに対するP' の相対変位である.
変位成分の増分値を
\[ du_{i} = \sum_{j}\frac{\partial u_{i}}{\partial x_{j}} dx_{j} \tag{14} \]
のように表したとき, ひずみ成分は次の式で定義される.
\[ \epsilon_{ij} = \frac{1}{2}\left(\frac{\partial u_{j}}{\partial x_{i}} + \frac{\partial u_{i}}{\partial x_{j}} \right) \tag{15} \]
(15)式のひずみは次の(A)~(C)の性質を持つ.
(A)伸びひずみ
$\epsilon_{ii}$ は, $x_{i}$ 方向の伸びひずみを表す(図3).
変形前, $dx_{1}$ 離れた2点間の距離が, 変形後は$dx_{1}'$ になったとすると
\[ dx_{1}' = dx_{1} + (u_{1} + du_{1}) - u_{1} \tag{16} \]
となる.
(B) 体積ひずみ
ひずみ成分の2次以上の積が無視できるとき
\[ \theta = \sum \epsilon_{ii} = \epsilon_{11} + \epsilon_{22} + \epsilon_{33} = div{\mathbf u}\tag{17} \]
は体積ひずみを表す.
変形前の体積
\[ dx_{1}dx_{2}dx_{3} \tag{18} \]
変形後の体積
\[ \begin{eqnarray} (1 + &\epsilon_{11}&) dx_{1}(1+\epsilon_{22})dx_{2}(1+\epsilon_{33})dx_{3} // &\approx& (1 + \epsilon_{11} + \epsilon_{22} + \epsilon_{33})dx_{1}dx_{2}dx_{3} // &=& (1+\theta)dx_{1}dx_{2}dx_{3} // \tag{19} \end{eqnarray} \]
ひずみ成分の2次以上の積が無視できるとき, 無限小ひずみと呼ぶ.
(C) ずりひずみ
$2\epsilon_{ij} (i ≠ j )$は, $x_i$ 軸と$x_j$ 軸の間のずりひずみを表す.
詳細は4-8-4を参照.
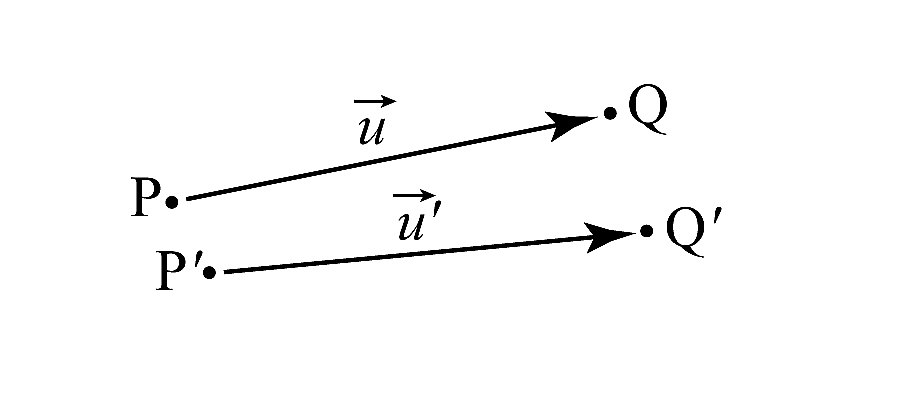
図3
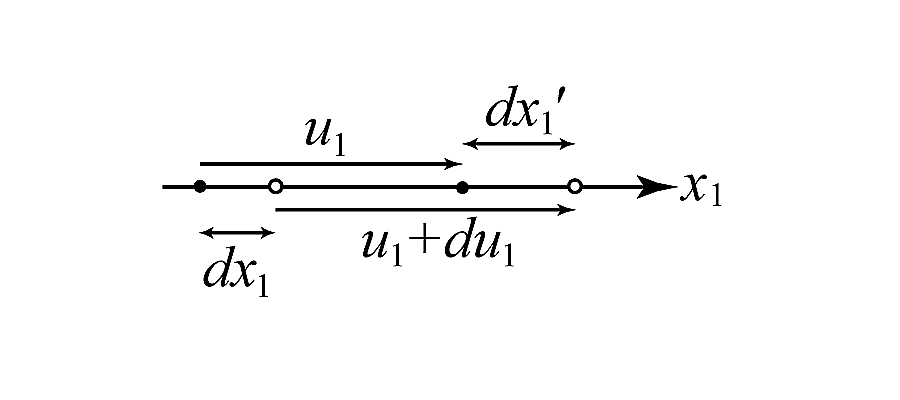
図4
4-8-3. 応力-ひずみ関係
応力成分とひずみ成分が次の関係を満たすものを等方弾性体と呼ぶ.
\[ \begin{eqnarray} p_{11}&=&\lambda\theta + 2\mu\epsilon_{11}, p_{12}=2\mu\epsilon_{12} // p_{22}&=&\lambda\theta + 2\mu\epsilon_{22}, p_{23}=2\mu\epsilon_{23} // p_{33}&=&\lambda\theta + 2\mu\epsilon_{33}, p_{31}=2\mu\epsilon_{31} // \tag{20} \end{eqnarray} \]
$λ$と$μ$をラメ定数と呼び, とくに$μ$を剛性率と呼ぶ.
(20)式を(13)式に代入してベクトル形式で表すと
\[ \rho\frac{\partial^2 u}{\partial t^2} = (\lambda+\mu) grad div{\mathbf u} + \mu\nabla^{2}{\mathbf u} \tag{21} \]
となる.(21)式の両辺の発散をとると
\[ \rho\frac{\partial^2 \theta}{\partial t^2} = (\lambda+2\mu) \nabla^2\theta \tag{22} \]
となる. すなわち, $\theta = div {\mathbf u}$ という状態が速さ
\[ V_p = \sqrt{\frac{\lambda + 2\mu}{\rho}}\tag{23} \]
で伝わる. これはP波を表している.
次に, (21)式の両辺の回転をとると
\[ \rho\frac{\partial^2 \Omega}{\partial t^2}=\mu\nabla^2\Omega \tag{24} \]
となる. すなわち, $\Omega = rot{\mathbf u}$という状態が速さ
\[ V_s=\sqrt{\frac{\mu}{\rho}}\tag{25} \]
で伝わる. これはS波を表している.
その他の定数
例1. 1軸方向圧縮の応力分布を考える(図3).
\[ p_{11} = P, p_{22} = p_{33} = 0, p_{ij} = 0 (i \neq j)\tag{26} \]
(20)式より$\epsilon_{ij} = 0 (i ≠ j )$ . ここで, $\epsilon_{11} = e , \epsilon_{22} = \epsilon_{33} = e’$とすると
\[ \begin{eqnarray} -\frac{e'}{e} = \frac{\lambda}{2(\lambda+\mu)} =\sigma :Poisson比// \frac{P}{e} = \frac{\mu(3\lambda + 2\mu)}{\lambda+\mu}=E :Young率 // \tag{27} \end{eqnarray}\]
となる.
例2. 静水圧の応力分布を考える.
\[ p_{11}=p_{22}=p_{33}=P, p_{ij}=0 (i \neq j)\tag{28} \]
\[ \frac{P}{\theta} = \lambda + \frac{2}{3}\mu = K \tag{29} \]
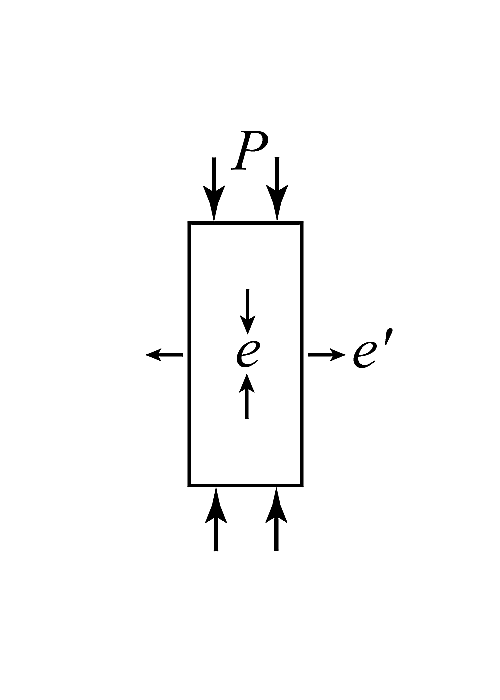
図5
4-8-4. ずりひずみ
ずりひずみ$2\epsilon_{ij} (i ≠ j )$ の意味について, $\epsilon_{12}$ を例にとって示す(図6).
変形前に直角を形成していた3点P, Q, Rが変形後にそれぞれP’, Q’, R’に変位したとする. $ {\mathbf P}{\mathbf P’}={\mathbf u} (u1 , u2 )$ とすると
\[ QQ' = {\mathbf u} + \frac{\partial {\mathbf u}}{\partial x_1}dx_1 = \left(u_1+\frac{\partial u_1}{\partial x_1}, u_2 + \frac{\partial u_2}{\partial x_2} \right) \tag{30} \]
である.
ここで, $P’Q’$が$x_1$軸となす角を$θ_1 , P’R’$が$x_2$軸となす角を$\theta_{2}$ とし, ともに微小量であるとする.
\[ \begin{eqnarray} \theta \tag{31} \end{eqnarray} \]
よって
\[ \tag{32} \]
となる.
すなわち, ずりひずみ$2\epsilon_{12}$は$x_1$軸と$x_2$軸の間の角度変化を表す.

図6

