4-7. 起潮力ポテンシャル

高知大学自然科学系 田部井隆雄

神奈川県温泉地学研究所 里村幹夫

京都大学大学院理学研究科 福田洋一

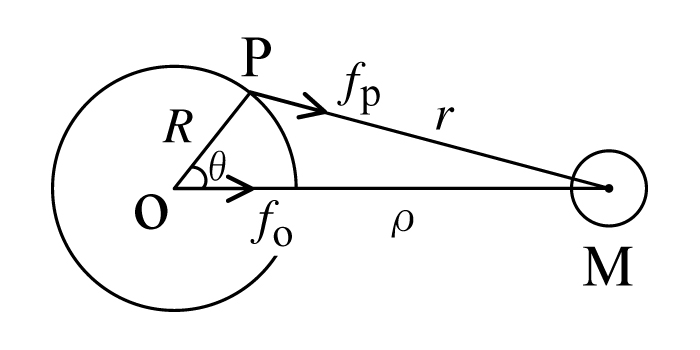
ある天体Mによる地球の重心O点での引力ポテンシャルは, 天体と地球の重心間の距離を$\rho$ とすると $GM/\rho$ である(図1). また, 地球の表面上の点Pでの引力ポテンシャルは, 天体の重心とP点との距離を$r$ とすると, $GM/r$ で与えられる. 点Pでの起潮力ポテンシャルW は, P点での天体による引力ポテンシャルから, 点Oでの引力ポテンシャルと点Oに働く力$f_o$ の点Pでのポテンシャル$｜f_o ｜\cos{\theta} ・R = GM・R\cos{\theta}/ρ^2$ を差し引いたものであるので

\[ W = GM \left( \frac{1}{r} - \frac{1}{\rho} - \frac{1}{\rho^2}R\cos{\theta} \right) \tag{1} \]

で与えられる. 次に, $r$を地球の平均半径$R$と天体との距離$\rho$で表すと

\[ r = \sqrt{\rho^2 +R^2 - 2\rho R\cos{\theta}}\\ \frac{1}{r} = \frac{1}{\rho} \sum_{n=2}^{\infty} \left(\frac{R}{\rho}\right)^n P_n(\cos{\theta})\\ \frac{1}{r} = \frac{1}{\rho} + \left(\frac{R}{\rho}\right)^n P_n(\cos{\theta}) \tag{2} \]

であり

\[ W = \frac{GM}{\rho} \sum_{n=2}^{\infty} \left(\frac{R}{\rho}\right) P_n(\cos{\theta}) \tag{3} \]

を得る. 特に$n=2$のとき, 2次のポテンシャル$W_2$は

\[ W_2 = \frac{GMR^2}{\rho^3}\frac{1}{2} (3\cos{\theta}^2 - 1) \tag{4} \]

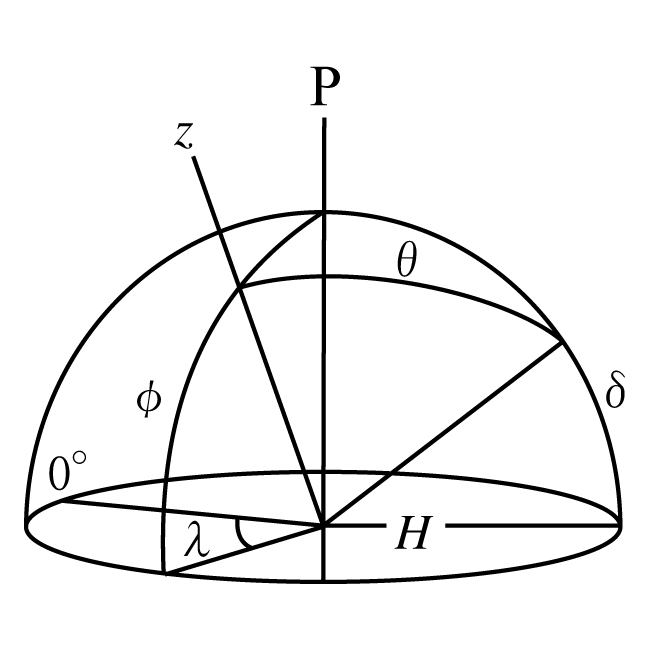
となる. 次に, 地心天頂距離と呼ばれる$\theta$を図2に示すように, 観測点の緯度$\phi$ , 経度$\lambda$ , 天体の赤緯$\delta$ , ならびに時角$H$ で表すことを考える. 球面三角法の余弦定理により

\[ \cos{\theta} = \sin{\phi}\sin{\delta} + \cos{\phi}\cos{\delta}\cos{H} \tag{5} \]

となる. 球面調和関数の加法定理より

\[ P_n(\cos{\theta} = \sum_{m=0}^{n}B_{nm}P_{n}^{m}(\sin{\delta})P_{n}^{m}(\sin{\phi})\cos{mH} \tag{6} \\ ただし, B_{n0} = 1, B_{nm} =2\frac{(n-m)!}{(n+m)!}, m \leq n \]

を用いると, 起潮力ポテンシャルは

\[ W = \sum_{n=2}^{\infty} Wn = GM\sum_{n=2}^{\infty} \sum_{m=0}^{n} B_{nm} \frac{R^n}{\rho^{n+1}} P_{n}^{m}(\sin{\delta})P_{n}^{m}(\sin{\phi})\cos{mH} \tag{7} \]

と表される. このうち2次のポテンシャル$W_2$は

\[ \begin{eqnarray} W_2 &=& GM \sum_{m=0}^{2} B_{2m} \frac{R^2}{\rho^3} P_{2}^{m} (\sin{\delta}) P_{2}^{m} (\sin{\phi}) \cos{mH} \\ &=& \frac{3GMR^2}{4\rho^3} \left\{ 3 \left( \sin^2{\phi} - \frac{1}{3}\right)\left(\sin^2{\delta} - \frac{1}{3} \right) + sin{2\phi}sin{2\delta}\cos{H} + \cos^2{\phi}\cos^2{\delta}\cos{2H} \right \} \tag{8} \end{eqnarray} \]

であり, ｛ ｝内の第1項が長周期潮(Zonal term), 第2項が日周潮(Tesseral term), 第3項が半日周潮(Sectorial term)を表す.

??1

??2