4-6. 物理測地学の基礎
高知大学自然科学系 田部井隆雄
神奈川県温泉地学研究所 里村幹夫
京都大学大学院理学研究科 福田洋一
4-6-1. ジオイド高とブルンズの公式
正規重力ポテンシャル$U$は, 回転楕円体上で$U = U_0 =constant$である. 一方, 地球の 重力ポテンシャル$W$で, $W = U_0$ となる等ポテンシャル面がただ1つ存在する. この等ポテンシャル面を ジオイドと呼び, 楕円体から測ったジオイドまでの距離$PQ = N$をジオイド高と呼ぶ. ジオイドは, 採用する楕円体パラメータ($a , f , GM , ω$ : ストークス定数)が与えられれば一義的に決まる. ジオイド上の点Pにおける重力ポテンシャル$W$(P)と標準重力ポテンシャル$U$ (P)の差
\[ T(P) = W(P) - U(P) \tag{1} \]
を重力乱れポテンシャルと呼ぶ(図1). $U$(P) は, 楕円体上の点Qにおける正規重力ポテンシャル$U$(Q)を用いて
\[ U(P) = U(Q) + \left(\frac{\partial U}{\partial n' }\right)_Q N = U(Q) - \gamma_Q N \\ W(P) = U(Q) -\gamma _Q N + T(P) \tag{2} \]
と表せるので, (1)は,
\[ W(P) = U(Q) = U_0 \tag{3} \]
となり, ジオイド高と重力乱れポテンシャルの関係を表したブルンズの公式
\[ N = \frac{T(P)}{\gamma_Q} \tag{4} \]
を得る.
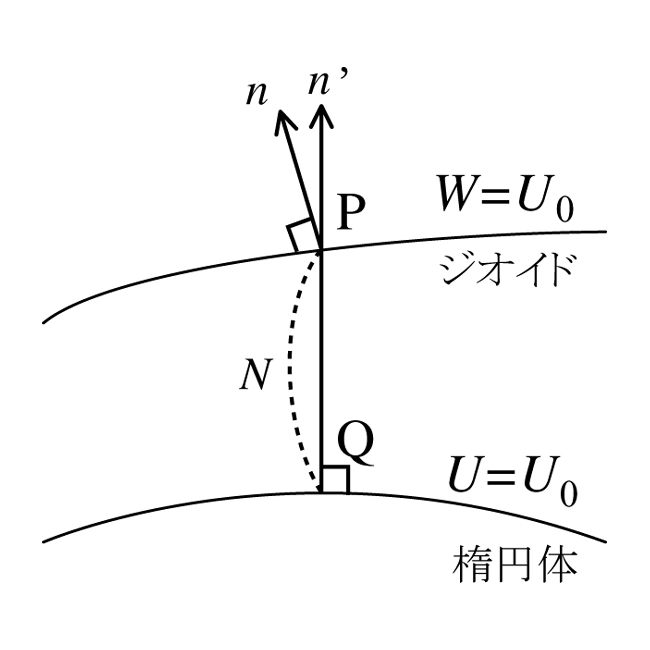
図1
4-6-2. 物理測地学の基本方程式
ジオイド上の点Pでの重力と, 楕円体上の点Qでの正規重力の差$Δg ≡g (P)-γ (Q)$を重力異常と呼ぶ(図2). $g (P)$は重力ポテンシャル$W$の点Pでの勾配であり, $γ (Q)$は正規重力ポテンシャル$U$の点Qでの勾配であるので, この関係を用いて書き改めると,
\[ \begin{eqnarray} g(P) & = & -\left(\frac{\partial W}{\partial n}\right)_P\\ \gamma(Q) & = & -\left(\frac{\partial U}{\partial n'}\right)_Q \simeq -\left(\frac{\partial U}{\partial n}\right) \simeq -\left(\frac{\partial U}{\partial n}\right)_P - \left(\frac{\partial \gamma}{\partial n}\right)_Q N\\ \Delta g & = & g(P) - \gamma(Q) = -\left( \frac{\partial W}{\partial n}\right)_P + \left(\frac{\partial U}{\partial n}\right)_P + N\left(\frac{\partial \gamma}{\partial n}\right)_Q \\ & = & -\left(\frac{\partial (W -U)}{\partial n}\right)_P + N\left(\frac{\partial \gamma}{\partial n}\right)_Q\\ & \simeq & -\left(\frac{\partial T}{\partial n}\right)_P + N\left(\frac{\partial \gamma}{\partial n}\right)_P \tag{5} \end{eqnarray} \]
を得る. ここで, ブルンズの公式(4)を用いると, 物理測地学の基本方程式
\[ \Delta g = -\left(\frac{\partial T}{\partial n} - \frac{T}{\gamma}\frac{\partial \gamma}{\partial n}\right)_P \tag{6} \]
を得る. 重力乱れポテンシャルT = W - U は, ジオイドの外でラプラス方程式
\[ {\nabla}^2 T = 0 \tag{7} \]
を満たし, (6)式は, ジオイド上での境界条件を与える.
図2
4-6-3. 球近似における物理測地学の基本方程式
重力異常など微小量について, 扁平率$f$を無視した近似を球近似と呼ぶ. このとき, 正規重力$\gamma$およびその勾配$\frac{\partial \gamma}{\partial n}$は
\[ \gamma = \frac{GM}{r^2}, \frac{\partial \gamma}{\partial n} = \frac{\partial \gamma}{\partial r} = -\frac{2GM}{r^3} = -\frac{2}{r} \gamma \tag{8} \]
であるので, (6)式は
\[ \Delta g = - \frac{\partial T}{\partial n} + \frac{T}{\gamma}\frac{\partial \gamma}{\partial n} = - \frac{\partial T}{\partial r} - 2\frac{T}{r} \\ \frac{\partial T}{\partial r} + \frac{2}{r}T + \Delta g = 0 \tag{9} \]
となる. 地球の平均半径を$R = (a^2b)^{1/3} $とすると, 重力乱れポテンシャル$T$は, $r > R$でラプラスの方程式
\[ \nabla^2 T = 0 \tag{10} \]
を満たし, (9)式は, $r = R$ の境界上で, $T$およびその1次導関数の1次結合$\Delta g$ として, ラプラスの方程式の 境界条件を与える. この境界条件の下に$T$を解く問題を第3境界地問題, または, 測地学において特にモロデンスキー問題と呼ぶ.
4-6-4. ストークス積分
球近似でのモロデンスキー問題
\[ \nabla^2 T = 0 \\ \frac{\partial T}{\partial r} + \frac{2}{r}T + \Delta g = 0 \tag{11}\]
を満たす$T$ は, 次のようにして得られる. 球座標でのラプラスの方程式の一般解は, $r >R$ で
\[ \begin{eqnarray} T & = & \sum_{n=2}^{\infty} \left(\frac{R}{r}\right)^{n+1} \sum_{m=0}^{n} (A_{nm}\cos{m \lambda} + B_{nm}\sin{m \lambda})P_{nm}(\sin{\psi}) \\ & = & \sum_{n=2}^{\infty} \left( \frac{R}{r} \right)^{n+1} \sum_{m=0}^{n} (A_{nm}R_{nm} + B_{nm}S_{nm}) =\sum_{n=2}^{\infty} \left(\frac{R}{r}\right)^{n+1} T_n(\theta, \lambda) \tag{12} \end{eqnarray} \]
である. 従って
\[\begin{eqnarray} - \frac{\partial T}{\partial r} &=& \sum_{n=2}^{\infty} \frac{n+1}{r} \left(\frac{R}{r}\right)^{n+1} T_n(\theta, \lambda) \\ - \frac{2}{r} T &=& \sum_{n=2}^{\infty} -\frac{2}{r} \left( \frac{R}{r} \right)^{n+1} T_n(\theta, \lambda) \tag{13} \end{eqnarray}\]
である. これらを(12)式に代入すると
\[ \Delta g = -\frac{\partial T}{\partial r} - \frac{2}{r} T = \frac{1}{R} \sum_{n=2}^{\infty} (n+1) T_n(\theta, \lambda) \tag{14}\]
を得る. 次に, $A_{nm}$ , $B_{nm}$ を求めるために$R_{nm}$ , $S_{nm}$ を両辺に掛けて, 球面調和関数の直交関係を用いると
\[\begin{eqnarray} A_{n0} &=& \frac{2n+1}{4 \pi} \frac{R}{n-1} \iint_{\sigma} \Delta g P_n(\theta', \lambda)d \sigma' \\ \left( \begin{array}{ccc} A_{nm} \\ B_{nm} \end{array} \right) &=& \frac{2n+1}{2 \pi} \frac{(n-m)!}{(n+m)!} \frac{R}{n-1} \iint_{\sigma} \Delta g \left( \begin{array}{ccc} R_{nm}(\theta', \lambda') \\ S_{nm}(\theta' \lambda') \end{array} \right) d\sigma' \tag{15} \end{eqnarray}\]
(15)式を(12)に代入し, 球面調和関数の加法定理を用いると
\[\begin{eqnarray} T(\theta, \lambda) &=& \sum_{n=2}^{\infty} \frac{2n+1}{4 \pi} \frac{R}{n-1} \iint_{\sigma} \Delta g \left\{ P_nP'_n + \sum_{n=2}^{n} \frac{2(n-m)!}{(n+m)!}(R_{nm}R'_{nm} + S_{nm}S'_{nm}) \right\} d \sigma'\\ &=& \frac{R}{4 \pi} \iint_{\sigma} \left\{ \sum_{n=2}^{\infty} \frac{2n+1}{n-1} P_n(\cos{\psi}) \right\} d \sigma' \tag{16} \end{eqnarray}\]
となる. ここで, ストークス関数を
\[ S(\psi) = \sum_{n=2}^{\infty} \frac{2n+1}{n-1} P_n(\cos{\psi}) \tag{17} \]
と定義すると
\[ T(\theta, \lambda) = \frac{R}{4 \pi} \iint_{\sigma} \Delta g (\theta', \lambda')S(\psi)d\sigma' \tag{18} \]
となり, さらにブルンズの公式を用いると, ストークス積分
\[ N = \frac{R}{4 \pi \gamma} \iint_{\sigma} \Delta g (\theta', \lambda') S(\psi) d\sigma' \tag{19} \]
を得る.

