4-3. ポテンシャル論の基礎
高知大学自然科学系 田部井隆雄
神奈川県温泉地学研究所 里村幹夫
京都大学大学院理学研究科 福田洋一
4-3-1. ニュートンの万有引力
距離$l$にある質量$m_1$, $m_2$の2つの質点間には, 質量の積に比例し 距離の2乗に反比例する万有引力が働き, その大きさ$F$は, $G$を万有引力定数とすると
\[ F=G\frac{m_{1}m_{2}}{l^{2}} \tag{1}\]
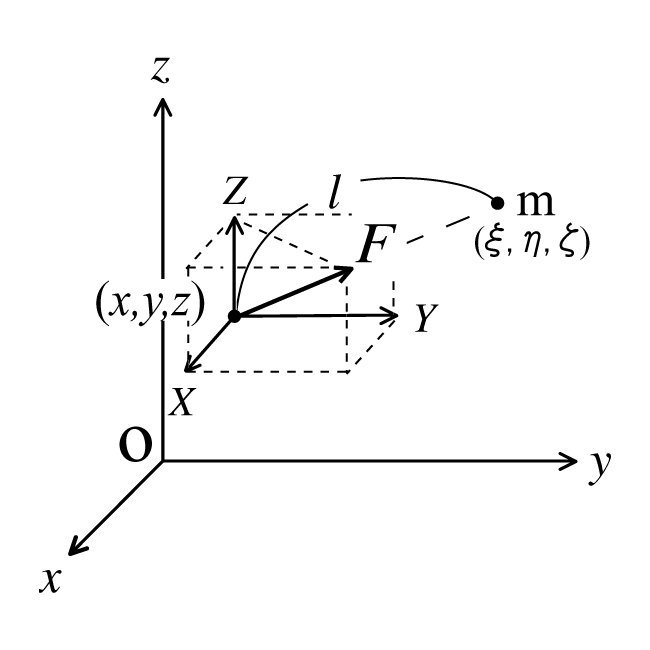
である. 直交座標系で, 座標$(\xi, \eta, \zeta)$にある質量$m$の質点が距離$l$だけ離れた点$(x, y, z)$に ある単位質量の質点に及ぼす力$F$の大きさは
\[ F=G\frac{m}{l^{2}} \tag{2}\]
であり, それぞれの$X, Y, Z$成分は
\[ \begin{equation} \begin{array}{l} X=-Gm\frac{x-\xi}{l^{3}}\\ Y=-Gm\frac{y-\eta}{l^{3}}\\ Z=-Gm\frac{z-\zeta}{l^{3}} \end{array} \end{equation} \tag{3}\]
となる. ただし
\[ l=\sqrt{(x-\xi)^2+(y-\eta)^2+(z-\zeta)^2}\tag{4}\]
である.
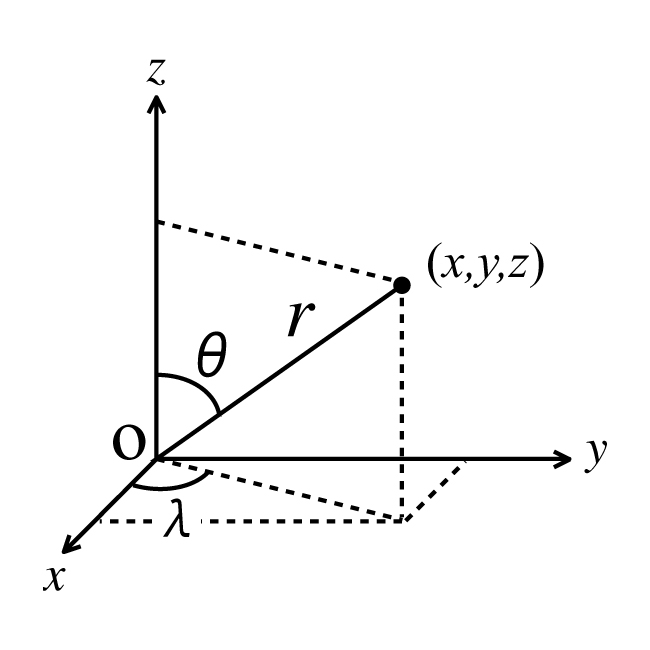
図1 図2 $V$をスカラー関数とすると, 単位質量に及ぼす力$F$が$V$の勾配$\mathrm{grad}V$で与えられるとき, すなわち \[ \mathbf{F}=(X,Y,Z)=\left(\frac{\partial V}{\partial x},\frac{\partial V}{\partial y},\frac{\partial V}{\partial z}\right)=\mathrm{grad}V \tag{5} \] を満たすとき, $V$を力$F$のポテンシャルと呼ぶ. \[ V=\frac{Gm}{l} \tag{6} \] とすると \[ \frac{\partial}{\partial x}\left( \frac{1}{l}\right)=-\frac{1}{l^2}\frac{\partial l}{\partial x}=-\frac{1}{l^2}\frac{x-\xi}{l} ... より \tag{6} \] \[ X=-\frac{\partial V}{\partial x}, Y=\frac{\partial V}{\partial y}, Z=\frac{\partial V}{\partial z} \tag{8}\] となる. $V$の勾配は, 力$F$に一致する. 従って, $V$は$F$のポテンシャルであり, これを質点の引力ポテンシャル(万有引力のポテンシャル)と呼ぶ. ポテンシャルはスカラー量であるので, 質量が連続的に分布する物体の引力ポテンシャル$V$は, 質点のポテンシャルの重ね合わせで与えられる. すなわち, 物体の微小部分の質量$dm$, 微小部分の体積$dv$での密度を$\rho$とすると, 連続体の引力ポテンシャルは, 微小部分の ポテンシャルを物体全体で積分することにより \[ V=G\iiint_v\frac{dm}{l}=G\iiint_v\frac{\rho}{l}dv \tag{9}\] で与えられる. 引力ポテンシャルV は, 質量がない場所で, ラプラス(Laplace)方程式 \[ \begin{equation} \begin{array}{l} \Delta V=\nabla^2 V=\mathrm{div} \mathrm{grad}V=0\\ \left(\frac{\partial^2}{\partial x^2}+ \frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right)V(x,y,z)=0 \end{array} \end{equation} \tag{10}\] を満たし, また, 密度$\rho$の質量のある場所で, ポワッソン(Poisson)方程式 \[ \begin{equation} \begin{array}{l} \Delta V=\nabla^2 V=\mathrm{div} \mathrm{grad}V=\rho\\ \left(\frac{\partial^2}{\partial x^2}+ \frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right)V(x,y,z)=\rho(x,y,z) \end{array} \end{equation} \tag{11}\] を満たす. $\nabla^2=\partial^2/\partial x^2+\partial^2/\partial y^2 +\partial^2/\partial z^2$ をラプラシアン(Laplacian)と呼ぶ. 直交座標でのラプラスの方程式の一般解は, $n , m$を整数, $A_{nm}, B_{nm}, C_{nm}, D_{nm}$を 実係数として \[ \begin{equation} \begin{split} V&=\sum\sum(A_{nm}\cos{(nx)}cos{(my)}+B_{nm}\cos{(nx)}\sin{(my)}\\ &+C_{nm}\sin{(my)\cos{(my)}}+D_{nm}\sin{(nx)}\sin{(my)})e^{-\sqrt{(n^2+m^2)Z}} \end{split} \end{equation} \tag{12} \] で与えられる. 一般に, ラプラスの方程式を満たす関数を調和関数と呼ぶ. 図6のように球座標$(r, \theta, \lambda)$を定義すると, 直交座標$(x, y, z)$との間に \[ \begin{equation} \begin{array}{l} x=r\sin{\theta}\cos{\lambda}\\ y=r\sin{\theta}{\lambda}\\ z=r\cos{\theta}\\ r=\sqrt{x^2+y^2+z^2}\\ \theta=\arctan{\frac{\sqrt{x^2+y^2}}{z}}\\ \lambda=\arctan\frac{y}{x} \end{array} \end{equation} \tag{13}\] の関係がある. このとき(10)式を座標変換することにより, 球座標におけるラプラスの方程式は \[ \Delta V=\frac{\partial^2 V}{\partial^2 r^2}+\frac{2}{r} \frac{\partial V}{\partial r}+\frac{1}{r^2}\frac{\partial^2 V}{\partial \theta^2}+\frac{1}{r^2\tan{\theta}}\frac{\partial V}{\partial \theta}+\frac{1}{r^2\sin^2{\theta}}\frac{\partial^2 V}{\partial \lambda^2}=0 \tag{14}\] となる. 図3 球座標におけるラプラスの方程式の一般解は \[ \begin{equation} \begin{array}{l}
V(r,\theta,\lambda) = \sum_{n=0}^\infty \frac{1}{r^{n+1}}Y_n(\theta,\lambda)\\
V(r,\theta,\lambda) = \sum_{n=0}^\infty r^n Y_n(\theta,\lambda)
\end{array} \end{equation} \tag{15},
\] であり, ここで, $Y_n (\theta, \lambda)$ は球面調和関数と呼ばれ, $n$ は任意の整数, $m$ は$n$ を超えない整数, $a_{nm}$ , $b_{nm}$ を任意の実定数として \[ \begin{equation} \begin{array}{l}
Y_n (\theta, \lambda) &= \sum_{m=0}^n (a_{nm}P_n^m(\cos \theta)\cos m\lambda + b_{nm}P_n^m(\cos \theta)\sin m\lambda)\\
&= \sum_{m=0}^n(a_{nm}R_{nm}(\theta ,\lambda)+b_{nm}S_{nm}(\theta ,\lambda))\\
&R_{nm}(\theta ,\lambda) = P_m^m(\cos \theta)\cos m\lambda\\
&S_{nm}(\theta ,\lambda) = P_n^m(\cos \theta)\sin m\lambda
\end{array} \end{equation} \tag{16},
\] である. 2つの球面調和関数の積を球面上で積分すると \[ \begin{equation}
\left\{
\begin{array}{l}
\iint_\sigma R_{nm}(\theta,\lambda)R_{sr}(\theta, \lambda)d\sigma \\
\iint_\sigma S_{nm}(\theta,\lambda)S_{sr}(\theta, \lambda)d\sigma
\end{array}
\right\} =0 \hspace{15pt} s≠n, または, r≠m \\
\iint_\sigma R_{nm}(\theta,\lambda)S_{sr}(\theta,\lambda)d\sigma = 0 \\
\left\{
\begin{array}{l}
\iint_\sigma [R_{nm}(\theta,\lambda)]^2d\sigma \\
\iint_\sigma [S_{nm}(\theta,\lambda)]^2d\sigma
\end{array}
\right\} =\frac{2\pi}{2n+1}\frac{(n+m)!}{(n-m)!} \\
ただし\\ \iint_\sigma [*]d\sigma=\int_{\lambda=0}^{2\pi}\int_{\theta=0}^{\pi}\sin{\theta}d\theta d\lambda
\end{equation} \tag{17} \] の関係が成り立つ. これを球面調和関数の直交条件と呼ぶ. 球面上で定義された任意の連続関数$f(\theta, \lambda)$は, 球面調和関数を用いて \[ \begin{equation} \begin{array}{l} f(\theta,\lambda)&=\sum_{n=0}^{\infty}{Y_n(\theta,\lambda)}\\
&= \sum_{n=0}^{\infty}\sum_{m=0}^{\infty}\left( a_{nm}R_{nm}(\theta,\lambda)+b_{nm}S_{nm}(\theta,\lambda) \right) \end{array} \end{equation} \tag{18}\] と展開できる. ここで, $a_{nm}$, $b_{nm}$は実定数であり, 両辺に$R_{nm}$, $S_{nm}$をかけて球面上で積分すると, 球面調和関数の直交条件より \[ \begin{equation}
\begin{array}{l}
a_{n0}=\frac{2n+1}{4\pi}\iint_{\sigma} {f(\theta,\lambda)P_n(\cos{\theta})}d\theta \\
\left[ \begin{array}{c} a_{nm} \\ b_{nm} \end{array} \right] = \frac{2n+1}{4\pi}\frac{(n-m)!}{(n+m)!}\iint_\sigma f(\theta,\lambda)\left[ \begin{array}{c} R_{nm}(\theta,\lambda)\\ S_{nm}(\theta,\lambda) \end{array}\right]d\sigma
\end{array}
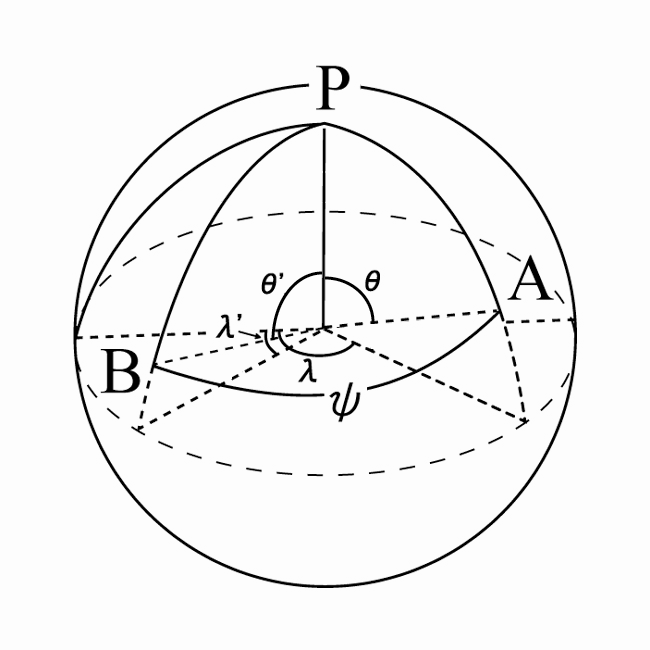
\end{equation} \tag{19}\] が得られる. 図4に示すように, 角距離$\psi$にある球面上の2点$A(\theta, \lambda)$, $B(\theta’, \lambda’)$, 極Pでつくる球面三角形PABにおいて成り立つ余弦公式 \[ \cos{\psi}=\cos{\theta} \cos{\theta'}+\sin{\theta}\sin{\theta'}\cos{(\lambda-\lambda')} \tag{20} \] を用いると \[ \begin{equation}
\begin{array}{l}
P_{n}(\cos{\psi})&=P_{n}(\cos{\theta}\cos{\theta'}+\sin{\theta}\sin{\theta'}\cos{(\lambda-\lambda')}) \\
&=P_{n}(\cos{\theta})P_{n}(\cos{\theta'})\\ &+2\sum_{m=1}^{n}\frac{(n-m)!}{(n+m)!}\left( R_{nm}(\theta,\lambda)R_{nm}(\theta',\lambda')+S_{nm}(\theta,\lambda)S_{nm}(\theta',\lambda')\right)
\end{array}
\end{equation} \tag{21} \] を得る. 図4 球座標系で表された角距離$\psi$にある2点$A(r , \theta , \lambda)$ , $B (r’ , \theta’ , \lambda’ )$の距離を $l$とすると, 余弦公式(20)により \[ l^2=r^2+r'^2-2rr'cos{\psi} \tag{22}\] が成り立つので, 1/l は, r > r' のとき \[ \frac{1}{l}=\frac{1}{r\sqrt{1-2(r'/r)\cos{\psi}+(r'/r)^2}} \tag{23}\] である. ここで, ルジャンドル関数の母関数を使うと \[ \frac{1}{l}=\sum_{n=0}^{\infty}\frac{r'^n}{r^{n+1}}P_{n}(\cos{\theta}) \tag{24}\] となり, また, 球面調和関数の加法定理(21)を使うと \[ \begin{equation}
\begin{array}{l}
\frac{1}{l}=\sum_{n=0}^{\infty}\frac{r'^n}{r^{n+1}}\left( P_n(\cos{\theta})P_n(\cos{\theta'}) \\
+2\sum_{m=1}^{n}\frac{(n-m)!}{(n+m)!} (R_{nm}(\theta,\lambda)R_{nm}(\theta',\lambda')+S_{nm}(\theta,\lambda)S_{nm}(\theta',\lambda'))\right)
\end{array}
\end{equation} \tag{24} \] を得る. 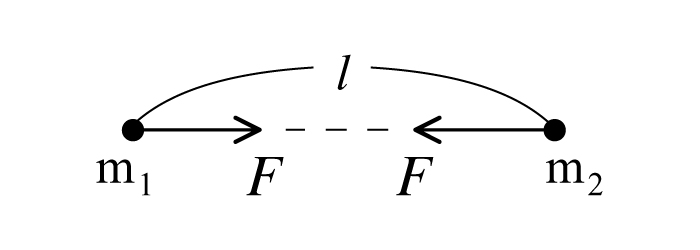
4-3-2. 力とポテンシャル
4-3-3. ラプラスの方程式
4-3-4. 球座標でのラプラスの方程式
4-3-5. 球面調和関数
4-3-6. 球面調和関数の直交条件
4-3-7. 球面調和関数による関数の展開
4-3-8. 球面調和関数の加法定理
4-3-9. $1/l$ の展開

