4-2. 球面三角法

高知大学自然科学系 田部井隆雄

神奈川県温泉地学研究所 里村幹夫

京都大学大学院理学研究科 福田洋一

単位球面(半径1の球面)上の3点ABC間を結ぶ大円が作る三角形を球面三角形と呼ぶ. 球面三角形では, 図3に示すように, 辺の長さa, b, cは 単位球の中心に対する角度で測り, A, B, Cは3辺の間の角度とする. このとき, 次の公式が成り立つ.

1. 正弦定理

\[ \frac{\sin{A}}{\sin{a}}=\frac{\sin{B}}{\sin{b}}=\frac{\sin{C}}{\sin{c}} \tag{1} \]

2. 余弦定理

\[ \cos{a}=\cos{b}\cos{c}+\sin{b}\sin{c}\cos{A}, \tag{2} \]

3. 正接定理

\[ \frac{\sin{C}}{\tan{A}}=\frac{\sin{b}}{\tan{a}}-\cos{b}\cos{C} \tag{3}\]

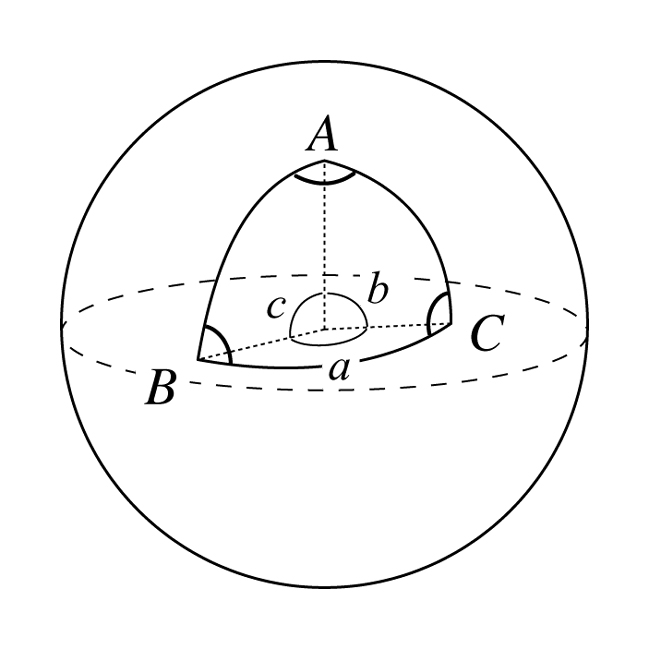
図3