4-1. 楕円体の幾何学

高知大学自然科学系 田部井隆雄

神奈川県温泉地学研究所 里村幹夫

京都大学大学院理学研究科 福田洋一

楕円は, 2定点(焦点F, F')からの距離の和が一定な点の軌跡である. 楕円の方程式は, 長軸半径をa , 短軸半径をb とすると

\[ \frac{x^2}{a^2}+\frac{z^2}{b^2}=1 \tag{1}\]

である(図1).

(1-1)の楕円をz軸の周りに回転させたときに得られる回転楕円体の方程式は

\[ \frac{x^2+y^2}{a^2}+\frac{z^2}{b^2}=1 \tag{2}\]

である(図2).

楕円または回転楕円体で, 焦点距離を$\overline{OF}$とすると

\[ \overline{OF}^2=a^2-b^2 \tag{3} \]

である.

焦点距離OF と長軸半径a の比を 離心率(eccentricity)e=OF/a , 短軸半径との比を第2離心率e'=OF/b と呼び, (1-3)式より

\[ e^2=\frac{(a^2-b^2)}{a^2} \tag{4} \]

\[ e'^2=\frac{(a^2-b^2)}{b^2} \tag{5} \]

である.

楕円の扁平率f は

\[ f=\frac{a-b}{a} \tag{6} \]

で定義され, 扁平率と離心率には

\[ e^2=f(2-f) \tag{7} \]

の関係がある.

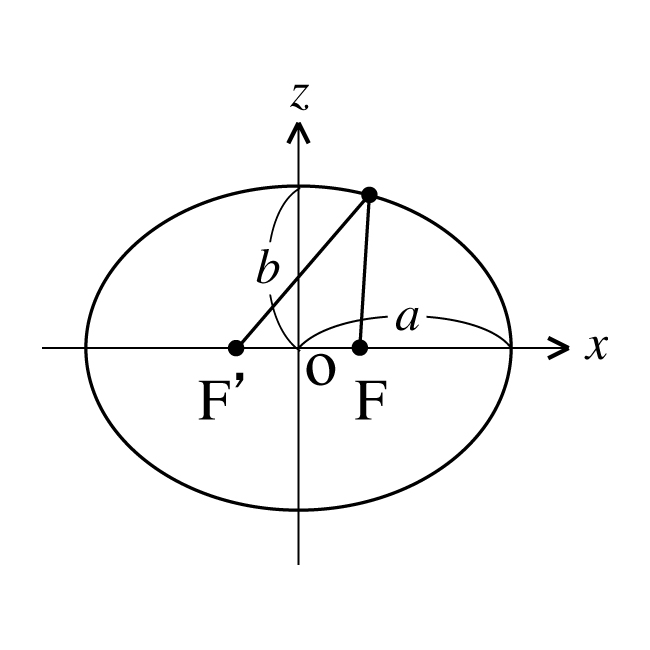
図1

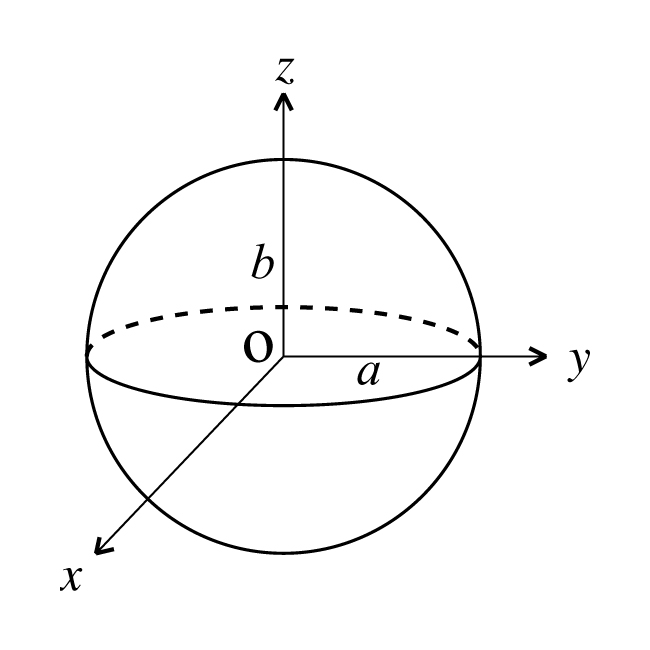
図2