2-4. 地球計測
高知大学自然科学系 田部井隆雄
神奈川県温泉地学研究所 里村幹夫
京都大学大学院理学研究科 福田洋一
2-4-1. 宇宙測地(*)
「宇宙測地」という用語は, 日本語としてやや奇異に思われるかもしれないが, より正確には, 宇宙技術を用いた精密測地計測一般を指す. 現在, 宇宙測地にはさまざまを手法が含まれるが, それらは, 地球上での位置計測を行うものと重力場を計測するものに大別することができる
位置計測に関連した宇宙測地技術の代表としては, VLBI(Very Long Baseline Interferometry, 超長基線電波干渉計), SLR(Satellite Laser Ranging, 人工衛星レーザー測距), GNSS(Global Navigation Satellite System, 全世界航法衛星システム)が挙げられる. これらは, いずれも, 基本的には地球上の2点間の距離(基線長)をたいへん正確に測定する技術であり, さまざまな測定点間での基線長データを調整することで, 地球上での3次元的な位置を決定している. これらは, 原理的には, 従来, 地上で行われていた三角測量や基線長測量などによる測地網測量の延長上にあり, 宇宙技術を利用することで, 地球規模での精密な位置決定を可能としているといえる. これらの技術は, また, VLBIが人工衛星を用いない天体からの電波を利用した測定, SLRがレーザー光を用いた地上からの測定, GNSSはその可搬性など, それぞれに固有の特徴を持ち, それらを生かした利用が進められている. 現在, いずれも, その測定精度はmmのオーダーに達している.
位置計測に関連した宇宙測地技術の1つとして, 最近, SAR(Synthetic Aperture Radar, 合成開口レーダー)の利用が注目されている. SARは, 元来, マイクロ波レーダーを用いたリモートセンシング技術として開発されたものであるが, 時期の異なるSAR画像の差を作成すること(干渉処理)で, 地殻変動を面的な画像の変化として検出することが可能である. この技術は干渉SARと呼ばれ, 地震や火山活動に伴う地殻変動の検出などに利用されている.
宇宙技術による地球の重力場の計測として, まず, 人工衛星の軌道追跡を挙げることができる. 衛星の軌道は地球の重力場の揺らぎを反映し少しずつ変化しているので, 軌道を精密に追跡することで, 逆に, 地球の重力場を知ることができる. SLRは, このような衛星の軌道追跡にも利用されている. この技術をさらに進めたものが衛星重力ミッションであり, 現在, CHAMP(Challenging Minisatellite Payload), GRACE(Gravity Recovery and Climate Experiment)ミッションが進行中で, 2009年3月には, GOCE(Gravity field and steady-state Ocean Circulation Explorer)も打ち上げられた(注*).
(*) CHAMPは2010年9月に運用停止した. GRACEとGOCEについては第3部を参照されたい.
直接的な重力場の測定ではないが, 海域の重力場の研究に欠かせないものとして, 海面高度計がある. 海面高度計は, マイクロ波レーダーにより衛星軌道から海面までの距離を正確に測る装置であるが, 海面の形状は, ほぼジオイドと考えてよいので, 海域のジオイドの形状, すなわち, 海域の重力場を測定することができる. 以前は, 観測船による測定に頼らざるを得なかった海域の重力異常のマッピングは, 海面高度計が利用されるようになり, 飛躍的な進歩を遂げている.
歴史的にみても, 天文観測が位置計測に重要な役割を果たしていたことは周知のとおりであり, 宇宙と測地学の関係は今に始まったものではないかもしれない. しかし, 現代の測地学は, 名実ともに宇宙測地技術なしには語れなくなっている.
2-4-1-1. GNSS
第3部「GPS近代化とマルチGNSS時代」で述べられているように,最近は日本も含めて世界の各国で人工衛星測位システムが構築されつつあり, それらを総称してGNSS(Global Navigation Satellite System)とよばれている. しかし現時点でもアメリカのGPS(Global Positioning System 全地球測位システム)が基本的な役割を果たしていることから, GNSSの基礎としてのGPSの仕組みについて理解しておくことが必要である.
GPSは, 複数のGPS衛星が発する電波を同時受信し, 受信点の3次元位置を決定する手法である. 利用形態は, 受信点の絶対位置を単独で決定する単独測位と, すでに位置が求められている基準点に対するもう一方の点の相対位置を決定する相対測位(干渉測位)の2つがある. 一般に, 単独測位は, 地球に対し静止または運動している物体の概略位置を求めるのに用いられ, 相対測位は, 静止点の精密位置を決定するのに用いられる. ただし, 地表の1点の静止位置を精密決定する精密単独測位や, 移動体の時々刻々の位置を相対測位によって決定するキネマティック測位などの手法もある.
GPS衛星は, 地表高度約20000kmの6つの軌道面に衛星が配置され, 現在はそれぞれに5個~6個ずつ, 約30個が投入されている(図1). 衛星は原子時計を搭載し, L1(1575MHz)およびL2(1228MHz)の2つの周波数の搬送波を, 衛星ごとに割り当てられたコードで変調し送信している. どのGPS衛星も同じ周波数の電波を用いているので, 受信機には, コードで変調された搬送波が混信して届く. 受信側では, 目的とする衛星のコードの逆パターンを生成し受信電波に積算する. 衛星から受信点までの電波伝播時間だけずらして積算したとき, コードによる変調が消え, もとの搬送波が再生される. この過程を通し, 混信した電波から目的の衛星の信号を取り出し, 衛星から受信点までの電波伝播時間を決定することができる. これに光速を乗じ, 衛星からの距離(擬似距離)を求める. 通常の単独測位では, 擬似距離が観測量となる. 相対測位では, 2点以上で搬送波の位相を同時観測し, 後処理操作において位相差を作成する. そのため, 相対測位は干渉測位とも呼ばれる.
衛星の動きは地球上の監視局によって追跡されている. 各衛星は, 送信電波に載せて, 数時間前までの衛星の運動から予測した現在位置を放送している(放送暦). これはリアルタイムで利用可能である. また, 衛星の運行から1週間程度遅れるものの, 地球上の多数の観測データから衛星が実際に運動した軌跡が精密に決定されている(精密暦). いずれにせよ, GPS測位では衛星位置は既知である. 単独測位では, 受信点は, 衛星を中心に擬似距離を半径とする球面上のどこかに位置する. 複数の衛星に対し同時に球面を描くと, 球面が交わる点が求める受信点の位置である. 相対測位では, 基準点に対し, 位相差の等しい点を結んだ等位相面が交わる位置が求める受信点の位置である. ただし, この場合は解の候補が多数存在するので, 何らかの方法によって真の解を決定する必要がある.

図1. GPS衛星の配置図(日本測量協会). 6つの軌道面に5個~6個ずつ, 約30個が投入されている
2-4-1-1-1. GPS単独測位(**)
単独測位の観測量である擬似距離は, コードによってもたらされる. コードとは, ある時間幅を最小単位とし, 0と1のいずれかの値が不規則に並ぶ擬似乱数列(Pseudo-Random Noise:PRN)である. コードの値が変化すると, 搬送波の位相は反転する(図2). GPSではC/Aコード, Pコードと呼ばれる2種類のコードが使われ, 最小時間幅はそれぞれ1μs ,0.1μsである. L1はC/AコードとPコードで, L2はPコードのみで変調されている. コード利用は, 衛星から受信点までの電波伝播時間の決定, 搬送波の再生, 受信電波の混信の解消, 機密性の保持, などの特徴を有している.
GPS受信機に内蔵された時計は, 衛星の原子時計と比較し, 精度が数桁劣る. つまり, 衛星原子時計が刻む電波の発信時刻は正確でも, 受信機で測定された到達時刻には大きな誤差が含まれている. ただし, ある瞬間に同じ受信機で複数の衛星の電波を同時受信すれば, 各々の測定値に含まれる時計誤差は同じ値となる. また, 短い時間内では, 時計誤差は一定値と見なせる. こうして, 受信点の3次元位置とともに, 受信機時計の誤差も未知量に加え, 4つの未知量を決定するために同時に4個以上の衛星からの擬似距離を利用する. この方法を, 単独測位と呼ぶ(図3).
単独測位は, ほぼリアルタイムに連続して行うことができる. 時計が時々刻々更新されることで, 受信機内部に仮想的な原子時計が出現する. 受信機の位置を求めるだけならば衛星は3個あればいいが, 時計を補正するためには最低4個が必要である. そのかわり, 受信側では原子時計を準備する必要がなく, 結果として, 受信機の小型軽量化, 低価格化が図られている.
単独測位の精度を決定する要因は, (1)衛星が放送している軌道情報の精度, (2)電離層および中性大気内での電波の伝播遅延, (3)コードによる擬似距離の分解能, (4)受信機時計の補正の不完全さ, 等である. (1)は数mと推定される. (2)に関して, 電離層の影響は, 太陽活動の極大期には10mを超えることがある. 中性大気のうち, 乾燥大気の影響は数m, 水蒸気の影響は乾燥大気の影響より小さいが, 時間空間変動が激しい. (3)と(4)は密接に関連する. 電波の伝播時間の測定精度はコードの最小時間幅と同程度なので, C/Aコード, Pコードの分解能は距離に換算してそれぞれ300m, 30mとなる.
以上を総合すると, 単独測位の精度は数10m~10m程度で, 車両, 船舶, 航空機などの航法支援には十分であるが, 一般に地殻変動観測の手法としては精度が不足する.
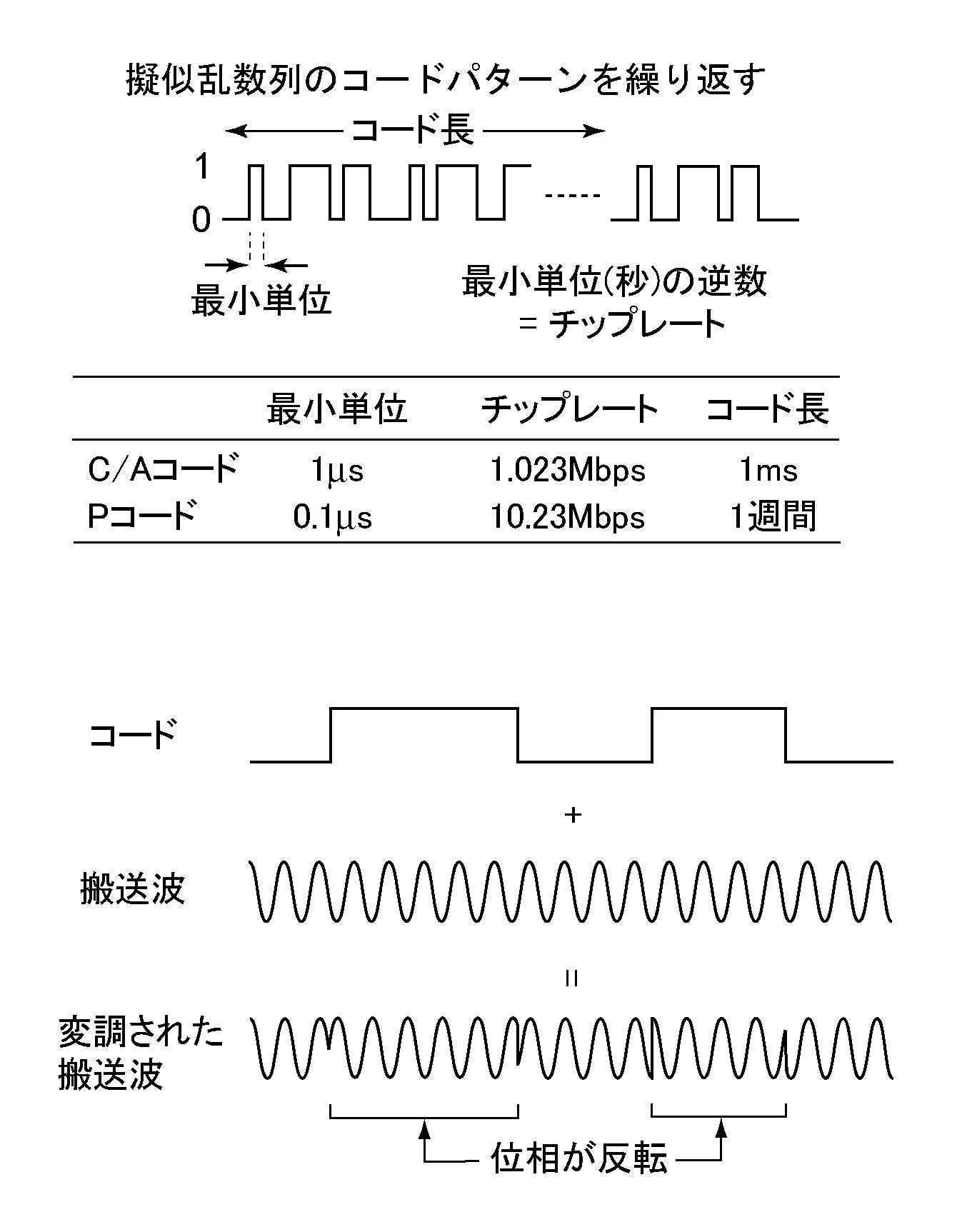
図2. GPSに用いられているPコード及びC/Aコード(上図)と, コードによる搬送波の変調(下図). コードの値が0と1の間で変化するとき, 搬送波の位相が反転する.
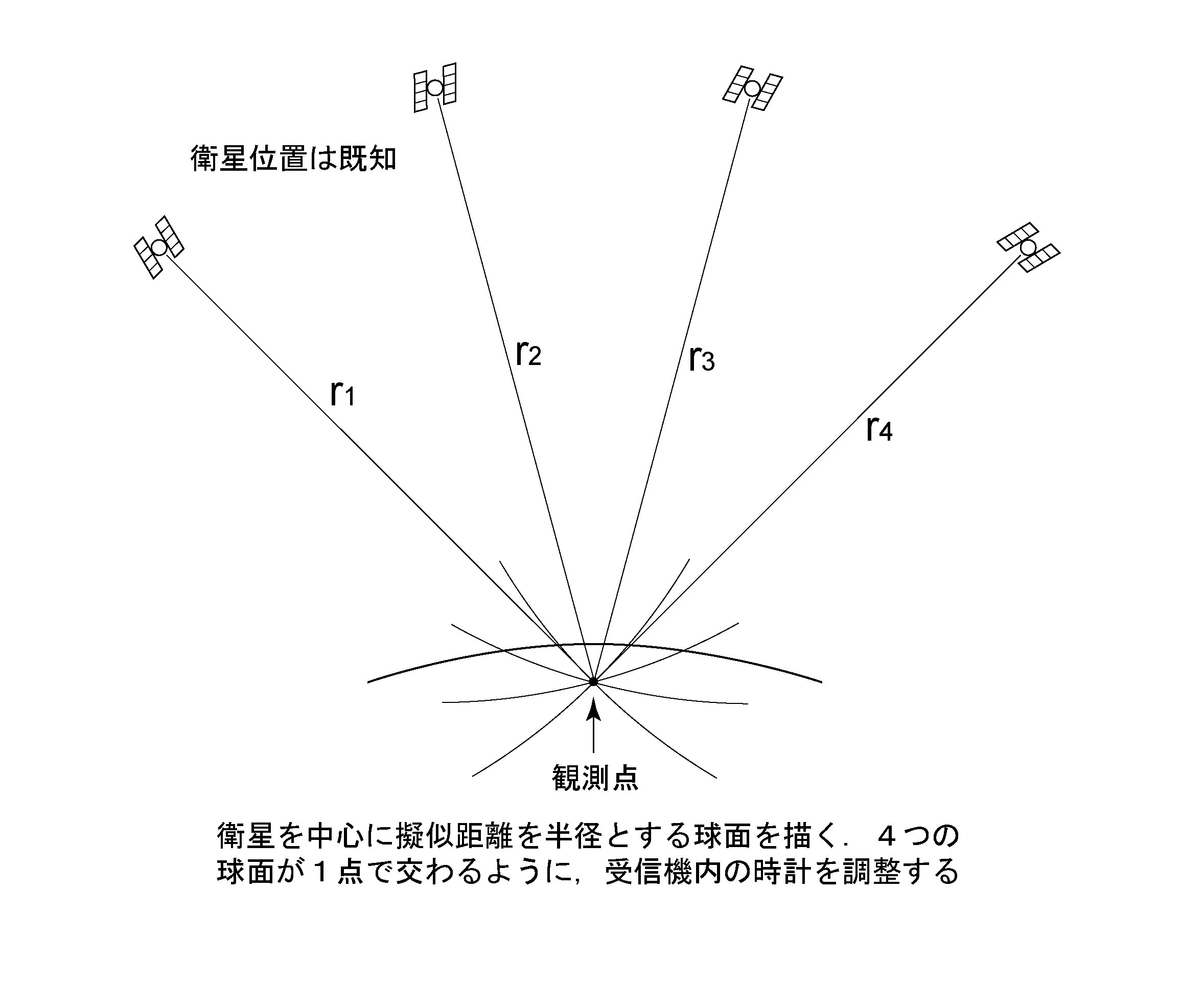
図3. 単独測位の概念図. 未知量は受信点の3次元位置と時計誤差の計4つである. 衛星を中心に擬似距離を半径とする球面の交点が求める位置である. このとき, 時計誤差に相当する量だけ, 各擬似距離は等しく補正されている.
2-4-1-1-2. GPS相対測位(**)
地殻変動観測のように, より高精度が必要な場合には, 相対測位を用いる. 相対測位では, 2地点以上で, 搬送波の位相を観測する. 搬送波の波長はL1が約19cm, L2が約24cmである. 1波長をさらに細かく分割して測定することが可能なので, コードによる距離測定に比べ, 分解能は非常に高い. ただし, 位相観測には2nπの不確定性があることに注意を要する.
観測終了後, 2地点で記録された位相の差を計算する. 例えば, 衛星1と点A, 衛星1と点Bの間の位相差を考える. 地表から衛星までの距離は観測点間の距離よりはるかに大きいので, 2つの経路は非常に接近している. 位相差をとることで, 衛星軌道のずれや経路上での電波伝播遅延はほとんど相殺される. これを一重差と呼ぶ. 同様に衛星2に対しても一重差を計算し, さらに一重差同士の差を計算する. これは二重差と呼ばれ, 受信機の時計の誤差が完全に相殺される. 二重差は相対測位の基本観測量で, 測位計算に入る前に誤差要因の大部分が除去されている. ただし, 決定できるのは観測点間の相対的な位置関係(基線ベクトル)のみで, 一方の座標値が既知である必要がある(図4). 位相の干渉を用いるので, 相対測位は干渉測位とも呼ばれる.
位相観測値には2nπの不確定性がある. 1つの衛星に対し, 位相の等しい点を結んでできる等位相面を, 1波長ずつずらしながら多数描くことができる. 他の衛星に対しても同様である. 等位相面の交点が観測点位置の候補となるが, 空間上に偽りの解が多数存在する. 衛星の移動とともに偽りの解も動くが, 真の観測点位置は不動のままである(図5). 位相不確定性の処理をいかに効率よく高速に行うかが, ソフトウェアの腕の見せ所である. この作業を「アンビギュイティを解く」, 「整数値バイアスを決定する」と言う.
長距離(>10km)で高精度の相対測位を行うには, 2周波の搬送波の利用と衛星の精密軌道情報(精密暦)の使用が必要になる. 電離層内での電波伝搬遅延は周波数の2乗に反比例するので, 2周波を用いると, これを推定し除去することができる. また, IGS(International GNSS Service)がグローバル観測データから作成している精密暦は10cmを切る精度を有しており, 高精度測位での利用が一般的になっている.
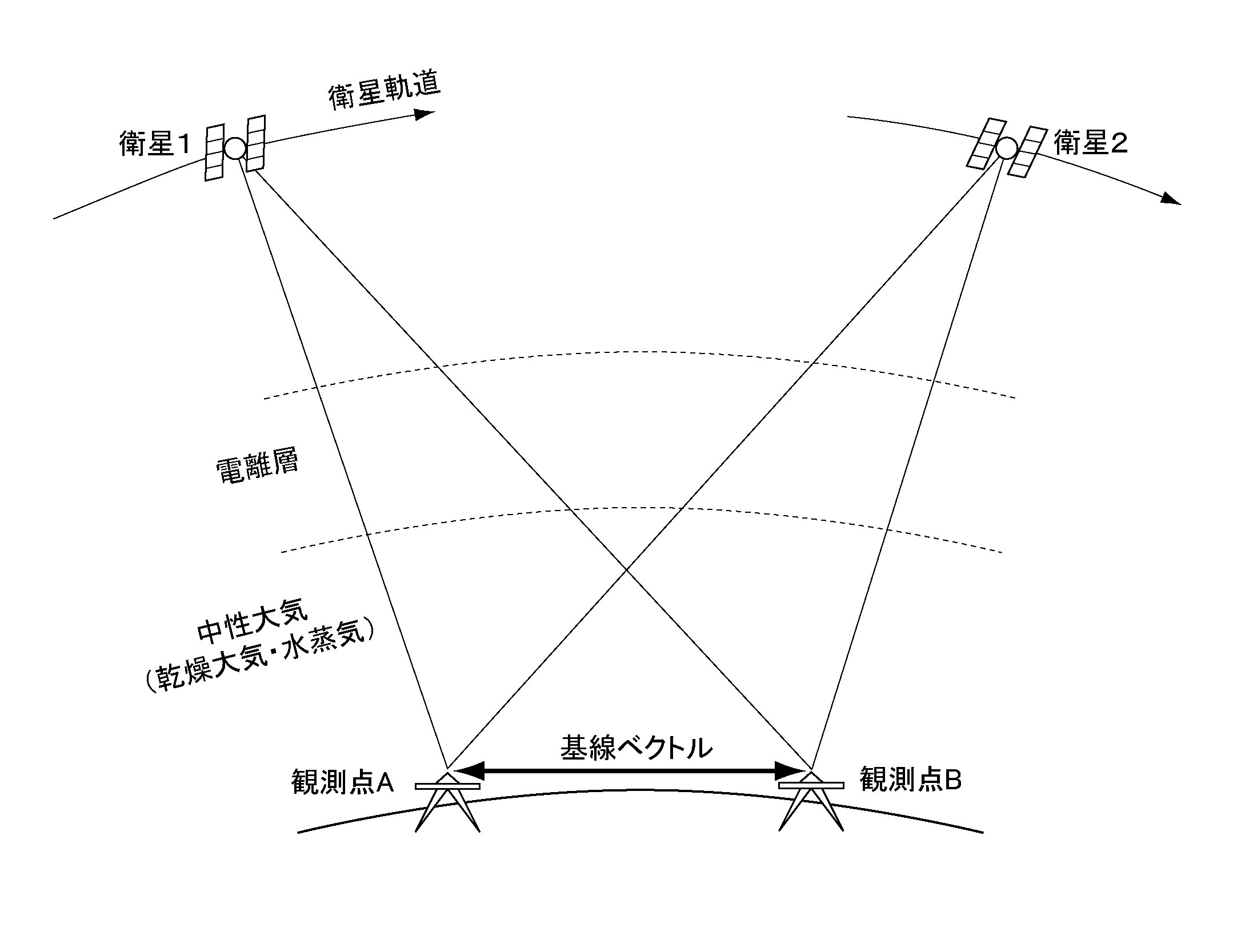
図4. 相対測位の概念図. 2つの衛星と観測点の間で二重の位相差を作成すると, 時計誤差は完全に, 衛星軌道のずれと経路上での電波伝播遅延はほとんどが相殺される. 二重位相差を用いて2観測点間の相対的な位置関係(基線ベクトル)を推定する.
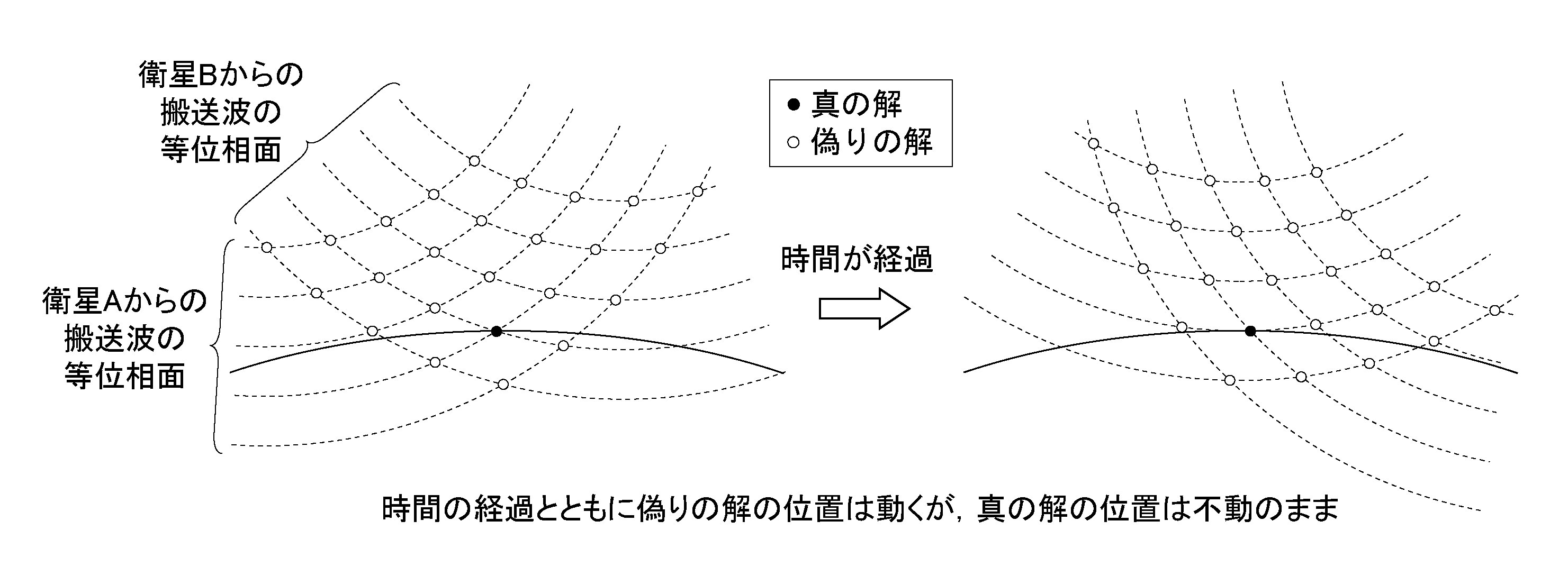
図5. 位相観測の不確定性. 搬送波の等位相面は1波長ずれた位置に多数存在する. 受信点の位置は等位相面の交点であるが, 偽りの解が多数存在する. 時間が経過しても, 真の解は不動のままである.
2-4-1-2. VLBI(*)
測地目的のVLBI(Very Long Baseline Interferometer, 超長基線電波干渉計)は, 地球から数億光年以上離れた準星(クェーサー)が発する電波雑音を受信し, 2点間の相対的な基線ベクトルを決定する手法である.
準星は十分遠方にあるので, 慣性基準座標系を与えると見なせる. また, 地球に到達する電波は, 平面波としての扱いが可能である. ただし, 電波の強度は極度に小さいので, 受信するには大口径のアンテナが必要となる. 一般に, 直径が数m~数10mのアンテナを用いる.
観測局では, 数GHzの周波数の白色電波雑音を, 高精度な周波数標準(原子時計)が出す刻時信号とともに記録する. 2つの観測局で受信した電波雑音の到着時刻にはずれがあり, この遅延時間を未知数として事後処理によって決定する. 遅延が存在した状態のままでは, 2つの雑音時系列の相関はつねにゼロである. 2つの時系列の時間軸を少しずつずらしながら相関を計算していくうちに, 真の遅延時間だけずらしたとき, 相関は突然1に近くなる. これは, 白色雑音といえども, 自己の複製との相関は1になるからである. 遅延時間が決定されれば, それに光速を乗じたものが幾何学的な遅延距離となる. 電波源の方向(赤緯と赤経)が既知であれば, 2点間の相対的な基線ベクトルを決定することができる(図6).
VLBIの利点は, 共通の電波源が観測できれば, 観測精度は原則として2点間の距離に依存しないことである. 実際には, 地球の曲率の影響で, 距離の増大とともに同じ電波源を観測する時間が短くなり, 結果として精度の低下が生じる. それでも, GPSなどと比較して, 長距離観測でも1cmを切る高い精度を有している. また, 準星を基準とするVLBIは, 地球の重心の位置や形状に依存しないという特徴をもつ. これは, 地球の重力場のもとを運動する人工衛星を基準としたGPSやSLRと, 事情がまったく異なる. VLBIの短所は, 装置の建設と維持に費用がかかり, 装置の可搬性もほとんど期待できないことである. 従って, 実際の運用面では, 大陸間や国家間の座標系の結合を主な目的とし, その隙間にGPS観測点を配置していく方法がとられている. 日常的に運用されているVLBI観測局は, 全世界で約30点ある(図7).

図6. VLBI観測の原理. 準星からの電波の到着時間差(遅延時間)から2つのアンテナ間の基線ベクトルが求められる.
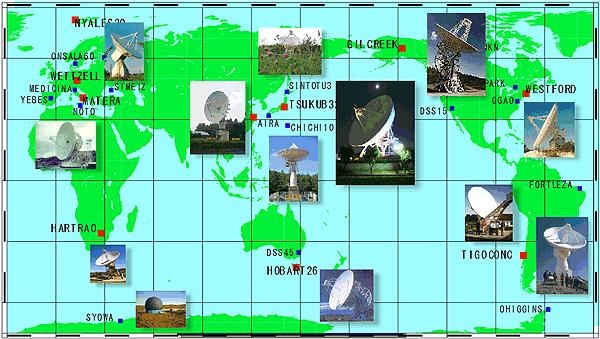
図7. 世界の主なVLBI観測局. (国土地理院ホームページ内「VLBIグループ」のページより)
2-4-1-3. SLR(*)
SLR(Satellite Laser Ranging, 人工衛星レーザー測距)は, 地表から人工衛星にレーザーパルスを照射し, レーザーが衛星表面で反射して地表へ戻ってくるまでの往復時間から, 地表と衛星の間の距離を測定するものである(図8). 衛星の軌道が既知であれば, 地表の3次元位置を決定でき, 逆に地表の位置が既知であれば, 衛星の軌道を決定できる.
SLR観測が行われている衛星の高度は, 数百km~約36000 kmまでさまざまである. 一般に, 低高度の衛星は詳細な地球の重力場の決定に適するが, 高度が低すぎると大気摩擦など軌道を乱す要因が大きく, 衛星の耐用年数が短い. 高高度衛星の軌道は安定しており, 地球の重力場の低次の項と密接に関係する. ただし, 信号強度は距離の4乗に反比例するため, 高高度衛星のSLR観測には大出力レーザー・大口径望遠鏡が必要となる. SLR衛星の表面にはコーナーキューブリフレクターと呼ばれる再帰型の反射鏡(図9)が多数貼り付けられており, レーザーは入射方向と平行な方向に反射される. 代表的なSLR観測専用衛星は, 直径が十数cm~約2mの球形をしている.
SLR観測の原理は単純であるが, 高精度を達成するためには数々の高度の技術を必要とする. はるか遠方を高速で飛翔する物体に連続してレーザーを照射し反射光を受信するには, 高精度の望遠鏡駆動システムが必要である.
SLRの観測精度はVLBIの精度に匹敵する. 費用の面や可搬性の点で問題があることも, 同様である. 相違点は, VLBIが地球の重心や形状にあまり依存しないのに対し, 人工衛星を用いるSLRは, これらに密接に関連していることである. ITRF(International Terrestrial Reference Frame, 国際地球基準座標系)は宇宙測地観測によって確立されているが, 地球の重心の位置とスケールは, SLR観測結果に基づいて決定されている. また, SLRは, アルティメーター衛星や他の地球観測衛星の軌道決定に用いられている.
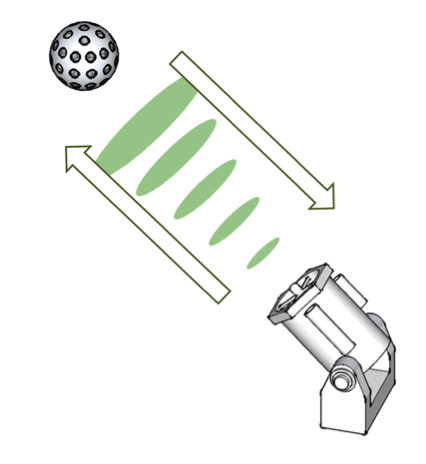
図8. SLR観測の原理. レーザーパルスの往復時間から地表と衛星との間の距離を求める. これを連続して行うことで, 衛星軌道と地表位置の関係が求められる.

図9. コーナーキューブ型再帰反射鏡のしくみ. 互いに直交する3面にて3回反射されることで, 光信号は来た方向に戻される.
2-4-1-4. SAR(*)
SAR(Synthetic Aperture Radar, 合成開口レーダー)とは, 人工衛星や航空機に搭載したアンテナを用いて地表に対しマイクロ波の照射と反射波の受信を連続的に行い, 空間上にあたかも巨大なアンテナが存在しているかのように, 高い分解能で地表の画像を得る技術である. 照射角がわずかに異なる複数のSAR画像を干渉させると, 地形高度を面的に決定することができる. 1枚目の画像が取得されてから, 2枚目の画像が取得されるまでに地殻変動が生じた場合は, 両者の干渉をとることで, 地殻変動の情報を引き出すことができる. これらの手法は干渉SARと呼ばれる. 地上に観測点を設置する必要がないという点が, GPS, VLBI, SLRと大きく異なる.
レーダーを真下に向けて照射すると, 進行方向に直交する両側の, 距離の等しい点からの反射波を区別することができない. これを避けるためSARでは斜め下に向けて送受信を行っており, サイドルッキングレーダーと呼ばれている(図10). 反射波の強度は対象物の物理的性質を, 位相は対象物までの距離の情報をもたらす. より正確には, アンテナと地表の間の距離をマイクロ波の波長で割った端数が位相である.
SARでは, 衛星や飛行機など飛翔体の運動する方向をアジマス方向, それに直交する方向をレンジ方向と呼ぶ. アンテナからは, 短い時間幅のパルスが送信される. この時間幅が狭いほど, 対象物までの距離を細かく測定することができる. SARでは以下に述べる「パルス圧縮」という手法を用いて, レンジ方向の空間分解能を上げている.
送信されたマイクロ波はアジマス方向にも幅を持っている. アンテナから送信される電波のビーム幅を$\delta \theta [rad]$, アンテナの大きさを$L [m]$, マイクロ波の波長を$λ [m]$とすると, 一般に$\delta\theta \fallingdotseq \frac{\lambda}{L}$ が成り立つ. 距離$R m$離れた位置でビームは$R\delta\theta [m]$の拡がりを持ち, これが空間分解能となる. 例えば, $\lambda=0.24 m$のマイクロ波を用いて$R=500 km$離れた対象物を$R\delta\theta=10 m$の分解能で判別したければ, $L=12 [km]$という大きさが要求される. このような巨大なアンテナを空間上に実現することは不可能である. そこで, 飛翔体が運動しながらマイクロ波を連続的に照射し, 同一の対象物から返ってくる反射波を適切に合成すると, 1つの巨大なアンテナで送受信を行ったのと同じ分解能を得ることができる. これが「合成開口」の原理である(図11).
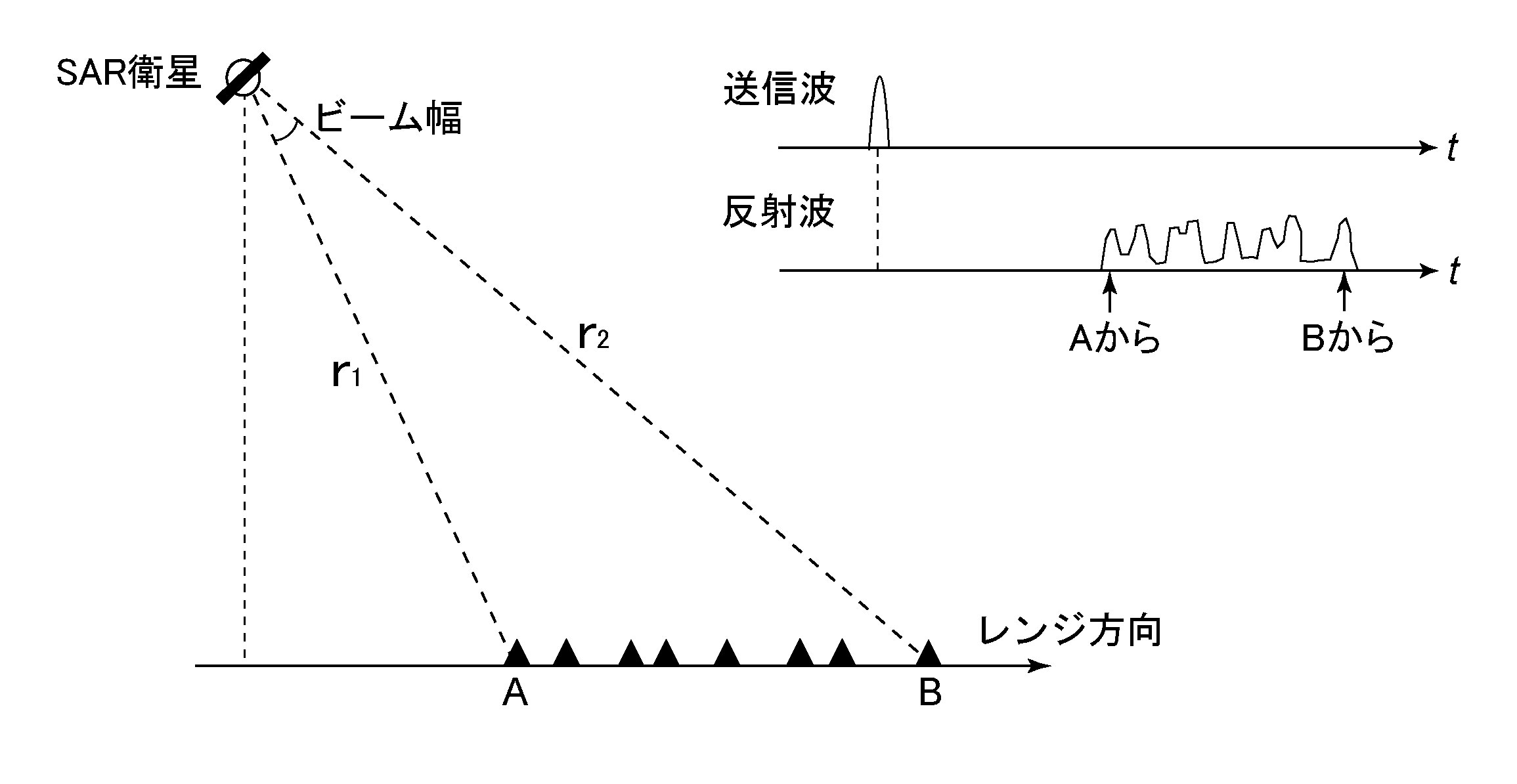
図10. サイドルッキングレーダーの原理. 衛星の進行方向と直交する方向(レンジ方向)に, 斜め下に向けてレーダー観測を行う. 衛星から対象物までの距離の違いに応じ, 反射パルスの到着時刻にずれが生じる.
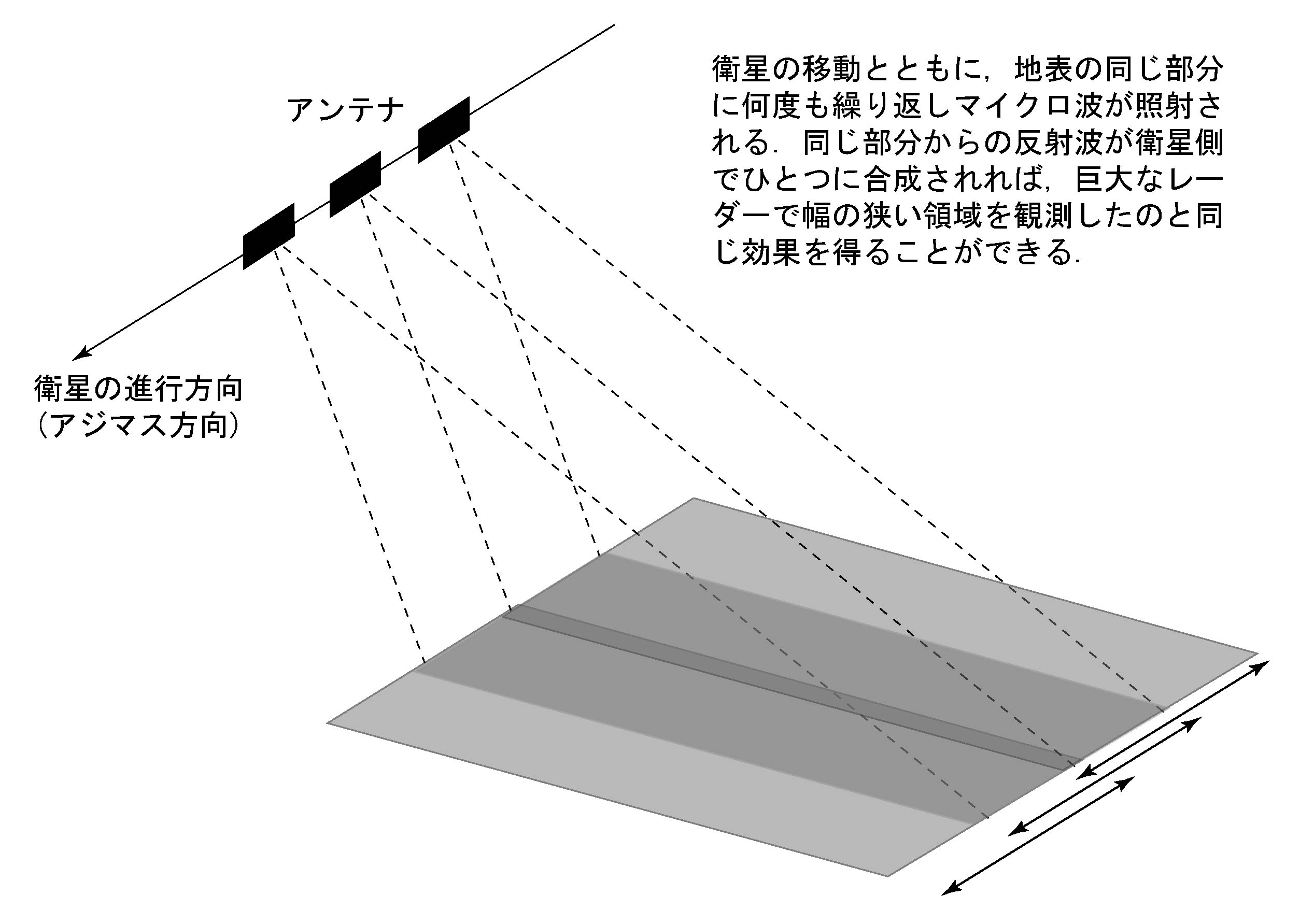
図11. アンテナの合成開口の原理. 地表の1点に注目すると, 運動する衛星から何度もパルスを受けている. 同じ点からの反射パルスを衛星側で系統的に積算すれば, 宇宙空間に巨大なアンテナを並べてパルスの送受信を行ったことに相当する.
2-4-1-4-1. パルス圧縮とアジマス圧縮(***)
マイクロ波の波長の10倍の径を持つアンテナを搭載した人工衛星が地表高度500kmを飛行し, 直下から$35^\circ$の角度で, 地表に向けて継続時間の短いパルスを照射する場合を想定してみよう. アンテナ径に対するマイクロ波の波長の比, すなわち電波のビーム幅($\delta\theta$)は$0.1 rad$(約$6^\circ$)となる($\delta\theta \fallingdotseq \frac{\lambda}{L} $). これが地表に達すると, レンジ方向に約75kmもの拡がりを持つ.
パルスは地表のさまざまな位置で反射して衛星に戻ってくるが, 衛星からの距離の違いに応じて, 到着時刻のずれが生じる. すなわち, 1回のパルス送信でも, レンジ方向の対象物の識別が可能である. パルスの時間幅が狭いほど対象物の識別能力は向上するが, 短い時間内に強度が十分大きい電波を送信することが困難になる. そこで, 周波数が時間の一次関数として増加するチャープ信号を, ある一定時間送信する. 受信した反射波に対しては, 周波数が時間の一次関数として減少する特性をもった整合フィルターと呼ばれるものを用いる. チャープ信号を整合フィルターに通した出力は, 振幅が増大しパルス幅が減少する性質を持つ. 結果として, 時間幅の狭い強力なパルスを送受信したのと同じ効果を得ることができる. この操作をパルス圧縮という.
衛星は運動しながら一定の時間間隔でパルスを発信している. アジマス方向にもビーム幅があるので, 地表の1点は, 少しずつ異なる角度で何度もパルスを受けることになる. ただし, 地表に対する衛星の相対運動のせいで, 反射波の周波数はドップラ効果により少しずつ変化する. すなわち, チャープ信号と同じ扱いが可能となり, 整合フィルターを用いれば, アジマス方向にビーム幅を絞ったときと同じ仮想的な出力を得ることができる. これは, $\delta\theta \fallingdotseq \frac{\lambda}{L}$の関係から, $\lambda$を一定のまま$\delta \theta$を小さくしたことになり, 結果としてL の値を大きくしたことになる. すなわち, あたかもアジマス方向にアンテナをいくつも並べたことに相当する. この操作をアジマス圧縮という.
2-4-1-4-2. 干渉SAR(**)
SAR衛星は一定の周期で同一軌道に回帰する. ある領域に対し1回目のSAR観測を行い, 異なる時期に, 同じ軌道から同じ領域に対し2回目の観測を行うものとする. はじめに, 2回の観測の間に地殻変動は生じていないものと仮定する. 一般に, 軌道は完全に同一ではなく, わずかにずれている. そのため, 衛星と地表の対象物との距離がわずかに異なり, 反射波位相も同じにはならない. 2つのSAR画像を干渉させると, 同位相の箇所で位相は強め合い, 逆位相の箇所で弱め合う. その結果, 位相差の等しい点を結んだ干渉縞模様ができる(軌道縞). これは, 2本の細い平行スリットを通った光が, 反対側の壁に干渉縞を作ることと類似している. さらに, SAR画像の干渉の場合には, 地表が平坦ではなく起伏(地形)を持っているために干渉縞がゆがんでいる. もし衛星の軌道情報が既知であれば, 軌道縞を理論的に計算し除去することで, 地形のみに起因する干渉縞(地形縞)を取り出すことができる. これを利用すると, 面的な地形標高モデルを作成することができる(図12).
2回のSAR観測の間に地表面が変動したときはどうなるだろうか? 衛星軌道情報から軌道縞は除去できるものとすると, 干渉画像には地形縞と, 地殻変動に起因する変動縞が混ざっている. もし地殻変動が生じていない時期の別の干渉画像が得られているとすると, 地殻変動を含む干渉画像との差を計算することで, 両者に共通した地形縞を除き変動縞を抽出することができる(図13a, 図13b). この方法を差分干渉SAR法と呼ぶ.
干渉SARによる地殻変動観測をGPS観測と比較すると, 最大の特徴は, 地上での活動を何ら必要とせず, 数10km四方の面的な地殻変動を一括決定できることである. ただし注意すべきことは, 求められる地殻変動は衛星と地表間の視線方向の成分であり, これに直交する方向に対しては感度がないことである. また, 干渉SARでは同じ軌道から観測された2つの画像を用いるが, 現在運用されているSAR衛星の回帰周期は数10日なので, それより短い地殻変動の時間変化を捉えることはできない.
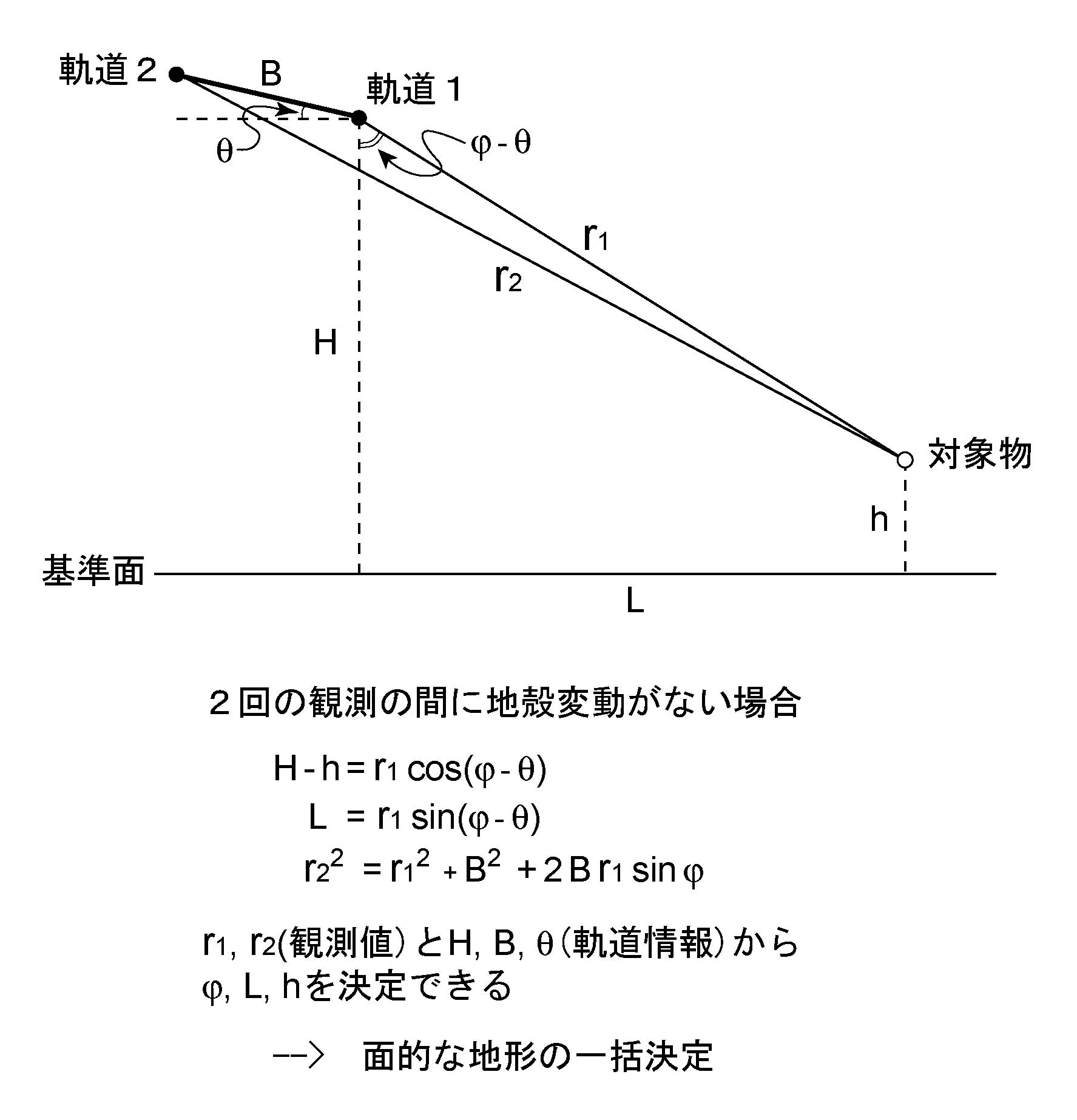
図12. 2つのSAR画像の干渉から地形を決定する原理. 衛星の軌道情報が既知であれば, 図に示した幾何学的関係より, 基準面からの個々の対象物の高さを決定できる.
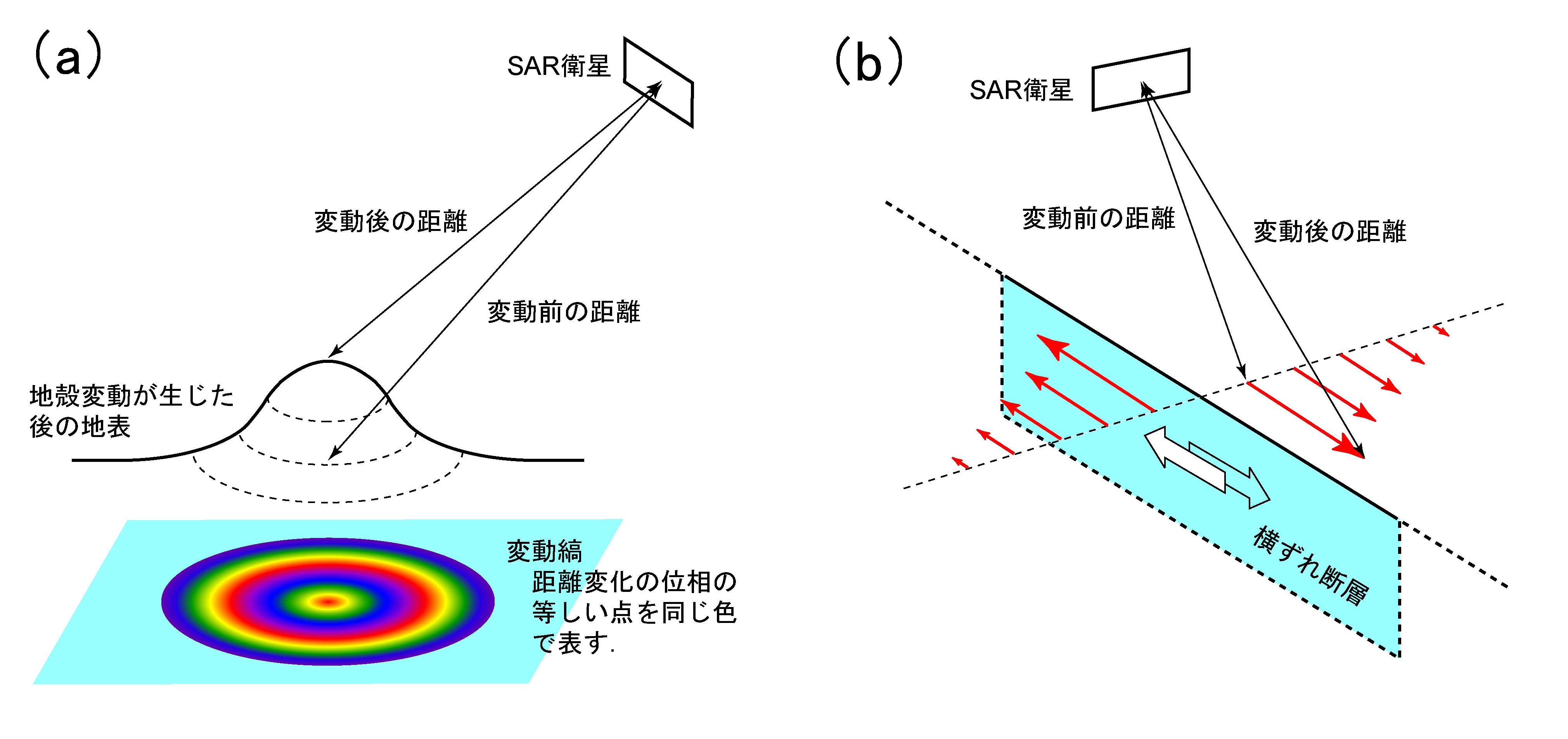
図13a. SARによる地殻上下変動の検出. 距離変化の位相が等しい点を同じ色で表すと, 地殻変動に応じた変動縞ができる. 図13b. 衛星と地表を結ぶ距離が変化すれば, 水平・上下を問わず, 地殻変動の検出が可能である.
2-4-1-5. 衛星高度計(*)
衛星高度計とは衛星軌道から地球表面までの距離を測る装置のことであり, 通常は, マイクロ波レーダーを用いた海面高度計のことを指すが, 現在では, 後述するICESat(Ice, Cloud and land Elevation Satellite)に搭載されているレーザー高度計もあるので, 用語の使用に注意が必要である. 実は, このような, 電波を用いたレーダー高度計か光を用いたレーザー高度計かといった測定方法の違いよりも, 海面の高さ(海面高)を測るのか氷床や陸地の高さを測るのかといった測定対象の違いの方が重要であり, 測地学的には海面高の測定が特別な意味を持っている. 海面高度計の原理はいたって簡単で, 図14に示すように, 衛星から発射したマイクロ波レーダーパルスが海面で反射して衛星に戻るまでの往復時間から, 衛星と海面との距離を測定するものである. このとき, 地球の重心を原点とした3次元直交座標系で, 衛星の軌道が正確にわかっているとすると, 楕円体から海面までの距離である海面高が得られる.
測地学にとって海面高度計データが特別な意味をもつのは, 海面の形状が, 重力の等ポテンシャル面であるジオイドの形に大変近いことによる. ジオイド高は, 全地球上で, ±100m程度の振幅を持っているが, 海面のジオイドからのずれはせいぜい1m程度であり, その1/100程度の振幅しかない. すなわち, 海面高度計は, 第1近似として, 海洋でのジオイド高を直接測定していると考えて差し支えない. ジオイド高がわかれば, それをもとに重力異常を計算することができる. さらに, 海域での重力異常の原因は, その大部分が海底地形によるものであるので, 海面高度計データから海底地形図を作成することも可能である. 実際, 船舶での観測が困難な海域でも, 海面高度計データを利用した詳細な海底地形図が作成されるようになっている.
最新の海面高度計データの精度は2~3cmと言われており, もはや, 海面の形状をジオイドとみなす近似が成り立たないことは明らかである. また, 海洋のダイナミクスと直接関連し, 海洋学的に意味があるのは, 海面とジオイドとの差として定義されるSSDT(Sea Surface Dynamic Topography, 力学的海面高度)である. SSDTの検出には, 海面高度計データとは別に重力異常から求めた高精度の重力ジオイドが必要であり, この分野では, 衛星重力データの利用に大きな期待が寄せられている.

図14. 海面高度計による海面高の測定.
2-4-1-5-1. 海面高度計の原理(***)
海面高度計では, マイクロ波レーダーを用いて衛星軌道から海面までの距離を測定するが, その精度は, レーダー波の往復時間をいかに正確に測るかにかかっている. 測定精度を向上させるためには, 大電力の鋭いパルスを作り出す必要があるが, 通常の方法では, パルス幅を狭めると送信電力も落ちてしまう. このため, 送信波として周波数変調された電波群を用い, 受信波を周波数領域において合成するチャープ圧縮という方法を用い, 送信出力を落とすことなく, 見かけ上, 鋭いパルスを作り出している.
図15は, ある幅を持つパルスが海面で反射して衛星で受信された場合の, 電波の受信強度の時間的変化を示したものである. 衛星から発射された電波の受信強度は, 海面での電波の反射面積に比例するので, 直下の海面からの反射を受信し始める図中のA点から増加をはじめ, パルスの後縁が直下の地点に達し, 反射面積が最大となるB点で最大となり, その後, 直下からの反射がなくなりC点に向かい徐々に減少する.
実際の海面高度計では, 多数のパルスの合成で平均的な受信強度曲線を得, A点とB点の中心点位置から, レーダー波の往復時間, すなわち測距データを得ている. さらに, レーダー波の反射の状況は電波が反射する衛星直下の海況を反映するので, 海面高度計の別の応用として, 受信波形の傾きから海面の波浪の状態や, また, 受信信号の強さから海上風の強さを推定することも可能である.
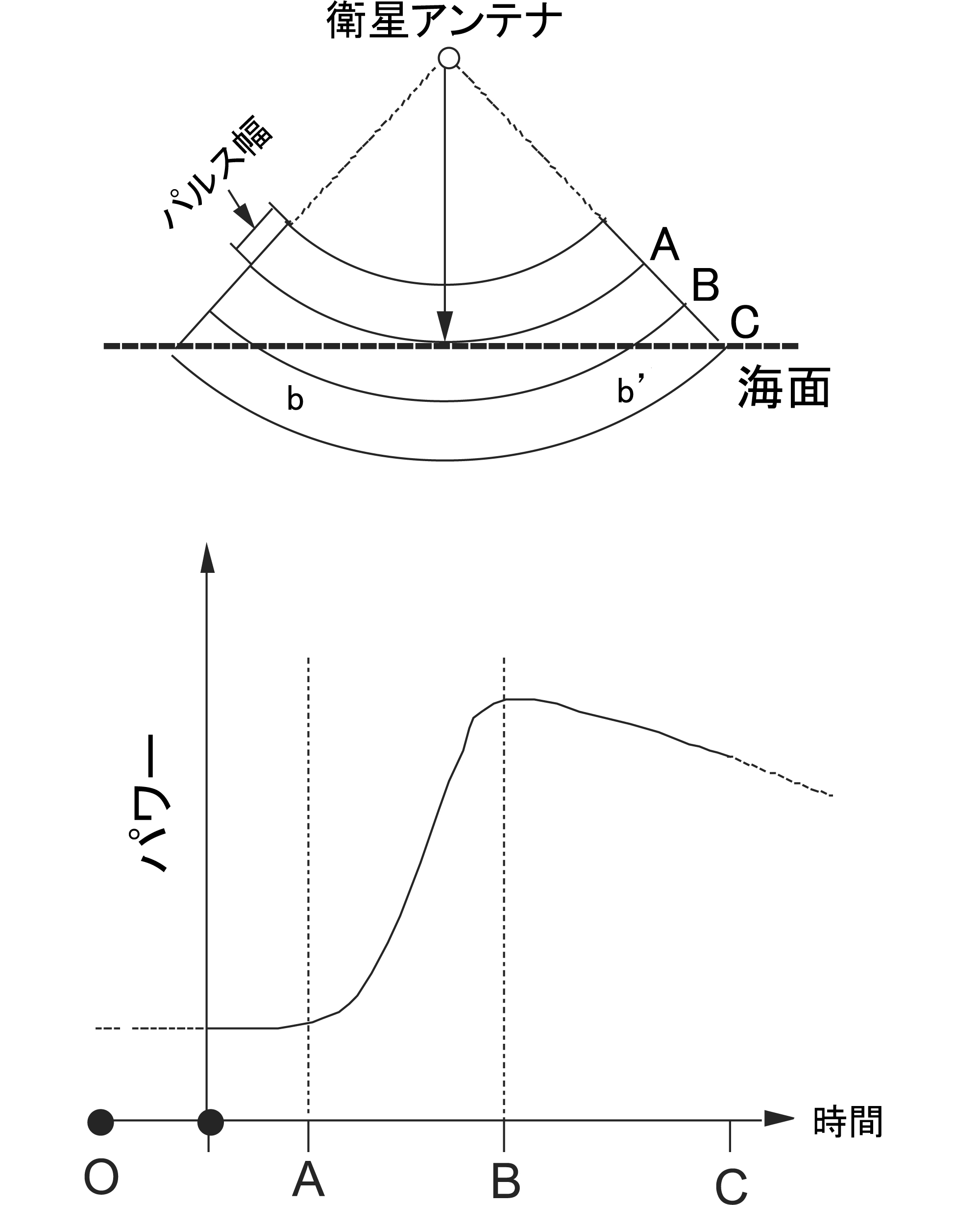
図15. レーダーパルスの反射強度の推移.
2-4-1-5-2. 海面高度計と海域の重力異常(**)
測地学における海面高度計データの利用で, 最も大きな成果をあげたのは, 海域での重力異常分布を明らかにしたことである. 1975年に打ち上げられたGEOS-3(Geodynamics Experimental Ocean Satellite)では, 3年以上の長期にわたり, 海面高の実用的なデータを取得した. GEOS-3は, 当初の予想をはるかに越えた多くの成果をあげており, 海域のジオイド, 重力異常や, その応用としてのテクトニクスの研究など, 多方面での利用がなされている. GEOS-3に続き, 1978年には海洋観測衛星SEASATが打ち上げられた. SEASATには, 分解能±10cmと, 高精度の海面高度計が搭載されていたが, 電源装置の不良のため, データが取得されたのは約3ヶ月間だけであった. しかし, それでも, 1980年代前半から中頃にかけ, GEOS-3やSEASATのデータを用いて, 相次いで海域の重力異常図が発表され, これらのデータは, その後のグローバルな球関数重力場モデルの改良にも大きく寄与している.
海域の重力場研究に最も大きく貢献したのは, 1985年3月に米海軍によって打ち上げられたGEOSAT(Geodetic Satellite)である. 特に, GEOSATの最初の18カ月間は, GM(Geodetic Mission)と呼ばれ, 海域の重力場の改良を主目的として, 全海域を出来る限る均質に覆うような軌道が選ばれた. 現在, GEOSAT-GMのデータに, ERS-1/2やTOPEX/Poseidon(T/P)などのデータも加え, 地球上のほぼすべての海域で, 大変詳細な重力異常図が作成され, また, それをもとに推定した海底地形図も公表されている.
従来, 測地学の1つの目的は, 重力異常からジオイドの形を求めることであった. しかし, 近似的とはいえ, 海面高度計で直接ジオイド高が得られるようになったことは, 物理測地学の根本に関わる革命的な出来事である. 具体的に, 海面高度計のデータから海域の重力異常を求めるためには, ジオイド高から重力異常への変換処理が必要である. これらの方法としては, 逆ストークス積分を用いる方法, 高度計データから垂直線偏差求めそれを逆ベニング・マイネス積分する方法, これらの計算をFFT(Fast Fourier Transform)を利用して空間周波数域で行う方法, 最小二乗コロケーション法などが用いられている.
海面高度計データと海底地形(NGDC Webサイト)

http://www.ngdc.noaa.gov/mgg/announcements/ announce_predict.html
2-4-1-5-3. 海面高度計と海洋変動(**)
海面の形状が等ポテンシャル面であるジオイドと一致しないのは, 海洋潮汐や海流, あるいは海水準変動など, 空間的にも時間的にも, 海洋がさまざまなスケールで変動しているためである. 海流と直接関係した力学的海面形状と呼ばれる海面高とジオイドとの差は, たかだか1m程度であるとはいえ, 現在, 海面高度計による海面高の測定精度は数cmに達しており, この差は十分測定可能な量である. このため, 現在では, 高度計データを利用した研究の中心は, 海域の重力異常の研究から, 海面高のジオイドからのずれやその時間的変化に関する海洋のダイナミクスの研究に移っている.
海面高度計データから正確な海流を推定しようとすると, その基準として, 重力ジオイドと呼ばれる重力データだけを用いたジオイドを精度よく決定する必要がある. しかし, 海面高度計の測定精度に見合う重力ジオイドを決めることは, 大変難しい問題である. 一方, 相対的な海面変動の研究には, 海面高度計のデータだけを用いればよく, このような目的に最も貢献したのは1992年に打ち上げられたTOPEX/Poseidon(T/P)である. T/Pは, 海洋学でメソスケールと呼ばれる空間波長数1000km, 周期数ヶ月程度の相対的な海洋変動の研究に多くの成果をあげたばかりでなく, 海洋潮汐モデルの改良や, 長期的な海水準変動のモニタリングなど, 海洋学のさまざまな分野で高度計データが有効であることを証明した. T/Pの後継機として, 2001年12月にJason-1が打ち上げられ, 現在では, 海況予報などの現業目的にも利用されつつある.
一方, 2000年以降, CHAMP(Challenging Minisatellite Payload)やGRACE(Gravity Recovery and Climate Experiment)など重力場測定衛星が打ち上げられ, 現在では, 重力ジオイドの精度も格段に向上しつつある. 特に2009年3月に打ち上げられたGOCE(Gravity field and Ocean Circulation Explorer)では, 重力ジオイドの精度として, 空間スケール100km程度で衛星高度計の測定精度に見合う1cmを目指しており, これは多くの海洋学的研究目的に十分な精度である. 海面高度計と衛星重力データは, 今後の海洋変動の研究にとって不可欠なものになるであろう.
関連Webサイト

2-4-1-5-4. 今後の海面高度計(**)
Jason-1の後続であるJason-2(*注)の計画では, WSOA(Wide-Swath Ocean Altimeter)と呼ばれる新しいタイプの高度計の搭載が検討されている. WSOAでは, 衛星の両側に長く張り出した2つのアンテナによる互いの海面反射波の干渉を用いて, 衛星軌道の直下ばかりでなく, その両側の面的な海面高度の測定が可能である. WSOAの主な目的は, 従来の海面高度計でとらえることが難しかった海洋の渦の研究にあるが, このようなデータが利用できるようになれば, 空間的に大変密なデータが得られることになり, 再び, 海洋における空間的に極めて高分解能な重力場の研究, あるいはそれを利用したテクトニクスの研究などにも寄与するものと期待できる. このほか, 将来型の衛星高度計の計画としては, 小電力, 軽量の小型衛星を同一のロケットで同時に多数打ち上げることで, 時間・空間分解能を向上させる計画や, より波長の短いKaバンド(26.5-40GHz)の電波を使った高度計で, 氷海, 氷床や沿岸域などの精度向上をねらった計画などもある.
この他, 衛星高度計としては, マイクロ波高度計ばかりでなく, SLRなどと同じくレーザー光による測距システムも利用される. 例えば, 我が国の月探査計画であるSELENE計画では, レーザー高度計(LALT)を用いた高度測定で, 精密な月面地形図を作製する計画である. また, 2003年1月に打ち上げられたICESat(Ice, Cloud and land Elevation Satellite)に搭載されているGLAS(Geoscience Laser Altimeter System)では, 波長532nmの緑色レーザーを用いた雲やエアロゾルなど大気の観測と同時に, 波長1064nmの赤外線レーザーを用い地形および氷床マッピングが行われている. 特に, 氷床マッピングの繰り返しにより, 氷床の流動を検出することも目的とされており, GRACEによる重力場変動データとあわせ, 南極やグリーンランドでの氷床変動の研究など, 今後の地球環境監視の1つの重要な柱になるものと大いに期待されている.
*注:Jason-2は2008年6月に打ち上げられたが, WSOAは搭載されなかった.
ICESat Webサイト

2-4-2. 重力測定(*)
重力の測定方法は, 大きく2つに分かれる. 1つは相対測定と呼ばれる方式で, 重力値が既知の地点との重力差や, あるいは, 同一の測定点での重力の時間的な変化だけを測定する方法である. もう1つは絶対測定と呼ばれる方式で, 文字通り, 測定点での重力の絶対値を測定する方法である.
歴史的には, 重力測定には重力振子, 特に2つの支点を持つ可逆振子(図16)が用いられ, 絶対測定のためには振子の長さと周期が, また, 相対測定には振子の長さは変化しないと仮定して, 周期だけが測定された. しかしながら, 可逆振子を用いた場合でも, 支点の位置に曖昧さが残る振子の長さの測定は大変困難であり, 重力振子による絶対測定では, 今日必要とされる高い精度での測定は不可能である. レーザー干渉計を用いた光学的な距離測定と, 原子時計による時間の計測技術が格段に進歩した現在では, 絶対重力測定としては, もっぱら, 落下する物体の落下距離と経過時間を直接計測し, 重力加速度を計算する方式が採用されており, 1~2μGalの測定精度が得られるようになっている.
一方, 相対重力測定においても, 1960年代頃までは重力振子も用いられていたが, その後, 第2次世界大戦後に油田開発など重力探査を目的として開発された小型のスプリング式重力計が広く普及し, さまざまな目的で用いられるようになった. スプリング式重力計では, バネの経時変化などの影響は避けられないが, 相対的には, 数μ~10μGalの測定精度が得られるうえに, 現在, 広く用いられているラコスト重力計やシントレックス重力計は, いずれも10kg程度と小型軽量で, バッテリー駆動で測定場所を選ばす, 簡便さでは絶対重力計をはるかにしのいでいる. このため, 野外での重力探査などでは, もっぱらスプリング式重力計による相対測定がなされている(図17).
このほか, 重力潮汐の観測など, ある点での重力の時間的変化だけを測定する目的には, 相対重力計の一種である超伝導重力計が用いられ, その感度は, nGalのオーダーに達している. また, 広範な地域の重力異常を知るためには, 船舶や航空機などを利用した重力測定も実施されているが, これらの目的にも, やはり相対重力計が用いられている.

図16. 可逆振子.

図17. ラコスト重力計を用いた, 野外での重力測定.
2-4-2-1. 絶対重力測定(**)
重力の絶対測定では, 真空中で投げ上げた物体, あるいは自由落下する物体の落下距離と経過時間から重力加速度を求める. 前者は投げ上げ方式, 後者は自由落下方式と呼ばれる. 投げ上げ方式の利点は, 落体に残留空気の抵抗が作用する場合でも, 投げ上げ時と落下時でその影響は逆方向に働き, 互いにキャンセルすることにある. しかしながら, 投げ上げ方式では物体の打ち上げにさまざまな工夫が必要で機構が複雑になることや, また, 真空技術の向上で高真空を維持することが比較的容易になり, 残留空気の影響をほとんど考える必要がなくなったことから, 最近では, 機構が単純な自由落下方式が主流となっている.
真空中を自由落下する物体の落下距離$x$, 経過時間$t$の関係は, 物体の初期位置を$x_0$, 初期速度を$v_0$, 重力加速度を$g$として,
\[ x=x_0+v_0t+\frac{1}{2}gt^2 \tag{1} \]
で与えられる. 一般に, 落体の初期位置, 初期速度を正確に決めることは困難なので, $x_0$, $v_0$も$g$と同時に決定することにすると, 落下中の3箇所以上で$(x,t)$を測定すれば, これら3つの未知数を決めことができる. これが自由落下方式の基本的な原理である.現在, 広く利用されているFG5絶対重力計(図18)では, 距離の測定にヨウ素安定化He-Neレーザーを用いたマイケルソン型のレーザー干渉計が, また, 時間の測定にルビジウム原子時計が利用されている. 図19はFG5絶対重力計で用いられている干渉計の原理を示したもので, 入射したレーザー光は, ビームスプリッターで2つの光に分割され, 一方のレーザー光(参照光)は直接フォトダイオードに, またもう一方の光は, 上部の自由落下するコーナーキューブ(一種の反射プリズム)で反射され, さらに, 下部に固定された参照用のコーナーキューブを経て, 同じくフォトダイオードに導かれる. このとき, 上部のコーナーキューブが自由落下することで, レーザー光の位相が連続的に変化するので, 図19に示すように参照光との位相があったとき, フォトダイオードの出力は最大に, また, 2つの位相が逆になったときに, 出力は0となる. したがって, フォトダイオードの出力が最大となる時間を原子時計で正確に測ることで, レーザー光の波長を長さの基準として, 落体の落下距離と経過時間を測定することができる. これにより, FG5絶対重力計では, 約0.2秒の落下中に, 600組程度の$(x,t)$の測定データを得ることができ, これらの測定データを, 上式にさらに重力勾配の補正項, 光の速度に対する補正項を加えた関係式に最小二乗法によりフィットさせることで, 重力加速度を計算している.

図18. 絶対重力計FG5.
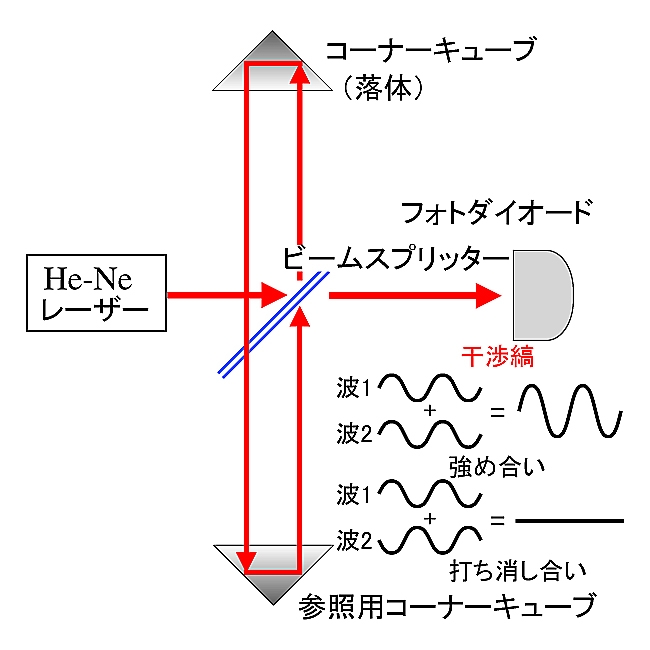
図19. 干渉計の原理.
2-4-2-2. 相対重力測定(**)
相対重力測定では, ある地点, あるいはある時刻での重力値を基準として, そこからの重力変化だけを測定すればよいので, 絶対重力測定のように時間と距離の両者について絶対値を測定する必要はなく, 測定の大幅な簡素化が可能である. 例えば, 重力振子を用いた測定でも, 相対重力測定の場合には, 振子の長さを一定で変化しないと考えれば, 振子の周期の測定だけでよく, 1960年頃までは, 重力振子を用いた測定も広く行われていた.
現在, 相対重力測定に用いられる重力計の多くはスプリング式重力計であり(図20), バネにつるした錘の位置が重力の変化によって変ることを利用し, 逆に, 錘の位置変化から重力の変化を求めるもので, 一種のバネばかりと考えることができる.
今, 重力を$g$, $k$をバネ定数, $m$を質量とし, バネの伸びを$s$とすると, フックの法則により,
\[ mg=ks \tag{2} \]
の関係が成り立つ(図20). 従って, 重力の変化⊿ g とバネの伸びの変化⊿ s の関係は,
\[ \Delta g=\frac{k}{m}\Delta s \tag{3} \]
であり, $\frac{k}{m}$が変化せず一定であると考えると, $\Delta s$から$\Delta g$を求めることができる.
このように, スプリング式重力計の原理は極めて簡単であるが, 要求される精度を達成するためには幾つかの問題点がある. その最大の要因は, 温度変化によるバネの伸び, あるいはバネ定数の変化である. これらの影響を少なくするため, バネの材質として, 線膨張率と弾性定数の温度係数の小さいインバール系の合金や溶融水晶が使われると同時に, バネそのものも温度制御された恒温槽に納められている.
このような温度変化の影響以外にも, スプリング式重力計では, ドリフトと呼ばれるバネそのものの経時的な変化による見かけ上の重力変化や, さまざまな機械的原因による重力測定値のトビもある程度は避けられない. このため, スプリング式重力計を用いた実際の野外測定では, データ処理でドリフトの補正が可能なように, 重力基準点から出発して各測定点での測定の後, 最初の基準点に戻る環測定や, それぞれの測定点で往路と復路で2回測定する往復測定(図22)などが実施されている. このように, 測定に細心の注意をはらうことで, 最近のスプリング式重力計を用いた相対測定では, 10μGalより良い測定精度が得られるようになっている.
地球潮汐の観測などに用いられている超伝導重力計(図23)も, 原理的には, 超伝導状態での永久電流磁場によるマイスナー効果(完全反磁性)をバネの復元力として利用した一種のスプリング式の相対重力計と考えてよい. 超伝導重力計では永久磁場の極めて安定な復元力, 極低温状態での物質の安定などが相まって, 従来のスプリング式重力計に比べ, 2~3桁の感度の向上と, 長期的な安定性を獲得している.

図20. スプリング式相対重力計の例(ラコスト重力計).
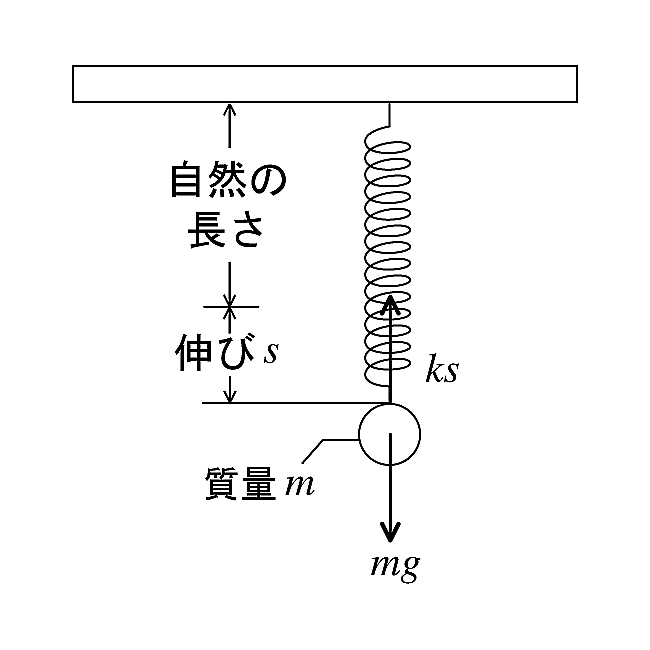
図21. バネばかり(バネ式相対重力計)の原理.
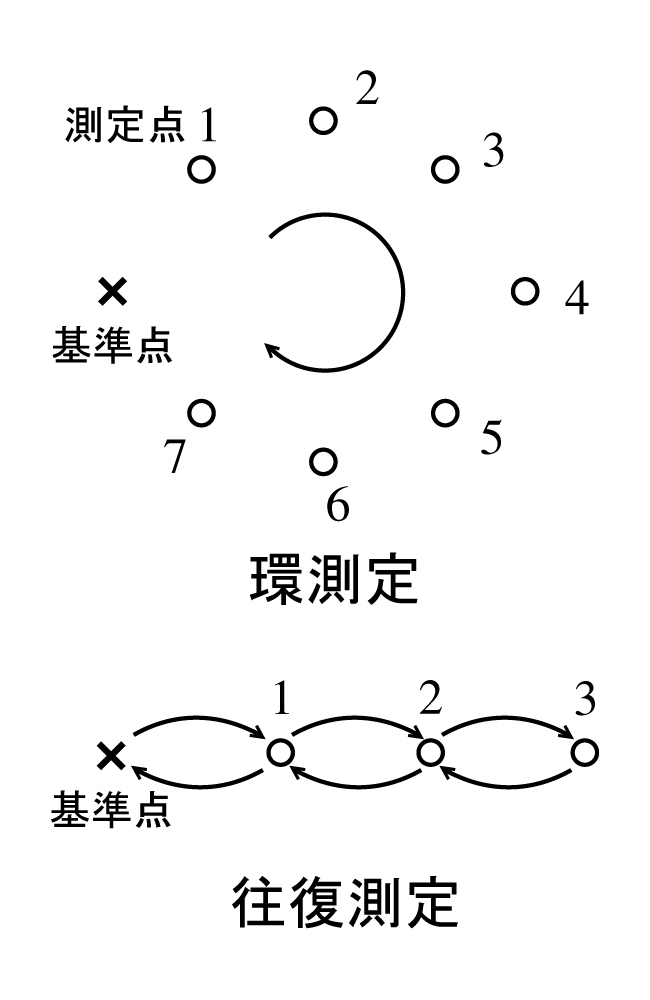
図22. 環測定, 往復測定の概念図. 環測定や, 往復測定を行うことで, 時間の関数と考えられる機器のドリフトを補正することが可能となる.

図23. マイスナー効果を利用した相対重力計である超伝導重力計.
2-4-2-3. 移動体上での重力測定(**)
陸上での重力測定は, 測定点に重力計を設置し, 重力計が静止した状態で行われる. 一方, 船舶や航空機に搭載された重力計では, 静止した状態ではなく, 航行中, あるいは飛行中に測定が行われる. このような移動体上での重力測定では, 陸上の重力測定と異なった幾つかの特殊性に考慮する必要がある.
まず, 船上重力測定について考えてみよう. 船上重力測定の特殊性の1つは, 船の動揺や振動である. 重力の測定は鉛直方向の加速度測定であり, ある瞬間の加速度に着目するかぎり, 測定点の上下加速度と, 重力加速度を区別することは不可能である. しかし, 船が航行することによる実際の重力の変化と, 船の振動や動揺による加速度では, その変動の周期が異なるため, 適当なフィルター処理で, 重力変化とその他の加速度とを分離することが可能である. 例えば1000トンクラスの観測船での鉛直の動揺は, 周期数秒~10秒程度で, 振幅は100~300Galにも達するが, このような動揺は周期が長くなるとともに急激に減衰し, 数10秒以上では0.1mGalよりも小さくなる. 一方, 重力の変化は, 100秒程度でせいぜい1mGalであるので, その周期以上のローパスフィルターをかけることによって, 重力加速度を分離することが可能となる.
船の動揺と関連してもう1つの重要な問題は, 重力計の鉛直方向をいかに保持するかということである. 重力測定では, 重力加速度のうち鉛直成分だけを測る必要があるが, 船の揺れで重力計が傾いた場合, 重力を正しく測定できない. このため, 船上重力計では, ジンバルや鉛直ジャイロなどの鉛直保持装置を用いている(図24).
移動体上での重力測定に関連した特有の現象としてエトベス効果がある. 赤道上を地球の自転と同じ東向きに, 速度$v$で航行する船上での重力測定を考えてみよう. この場合, 地球の半径を$R$とすると, 自転の角速度$\omega$が$\frac{v}{R}$だけ増えることになるので, 静止時との遠心力の差,
\[ \left(\omega + \frac{v}{R} \right)^2 R -\omega^2 R \fallingdotseq 2v\omega \tag{4} \]
だけ重力が減少したように見える(注). これは, コリオリ力の鉛直成分でありエトベス効果とよばれる. エトベス効果は見かけの重力変化であるので, その補正を行う必要があるが, そのためには船の対地速度$v$を正確に知る必要がある. 赤道上では, $v$を1ノット(約1.8km/h)としてもエトベス効果は約7.5mGalにもなるので, かつては, 船の位置から$v$をいかに正確に決めるかが船上重力測定の精度を決める1つの重要な要因であった. 現在ではGPSによる測位システムを利用することで, エトベス効果も十分な精度で計算されるようになっている.
航空重力測定では, 船と比較しはるかに速度が速いため, エトベス補正がより複雑になるほか, 航空機の移動による地球の重力の変化も大きく, 船のようなローパスフィルターを用いた動揺の補正もできなくなる. また, 高さが一定な海面上を航行する船と異なり, 飛行高度が変化する航空機上での重力測定では, 精密な高度の測定も必要となる. これらを補正するために, 航空重力測定では, 重力値とともに, 航空機の動揺や3次元的な位置を高精度で計測する必要がある. 航空重力測定で最も困難なのは, 実は, この位置の測定であり, 航空重力測定が真に実用化されるようになったのも, 精密GPS測位を用いた航法システムが出現して以後のことである.

図24. 船上重力計の例(NIPRORI-II 型).
注:緯度$\phi$で方位角$\alpha$に航行する場合のエトベス効果は, $2v\omega\cos\phi\sin\alpha$となる.
2-4-3. 地上での測地計測(*)
宇宙測地技術が一般に用いられるようになる前は, 位置の決定は, 三角測量, 光波測距, 水準測量といった地上での測地測量によりなされていた. 宇宙技術, とくにGPSの普及により, 三角測量, 光波測距といった主として水平位置を決めるための測定はあまり行われなくなったが, 比高を求める水準測量は, その精度の高さゆえ, 現在でもその地位は揺らいでいない.
地殻変動を求めるには, 同じ観測点でこれらの測地測量を繰り返し実施するのが1つの方法であるが, 他に, ある地点に地殻変動を連続的に測る計器を設置する方法がある. この種の計測器としては, 地面の傾斜変化を測る傾斜計, 地面の伸縮を測る伸縮計(ひずみ計), 体積変化を測る体積ひずみ計などがあり, これらの観測を総称して地殻変動連続観測と呼ぶ. また, 海面の高さを連続して測る検潮(験潮)も, 海面を基準として海岸の高さ変化を求めることができるので, 地殻変動連続観測の1つとして捉えることができる.
地殻変動連続観測は, 測地測量に比べ, 時間的に連続したデータが得られる利点があるが, 空間的には計器が設置された地点での変動しか得られないという弱点がある. また, 計器の長期安定性の問題から, 長期的な変動に関しては測地測量に比べてその信頼度が低いとされているが, 短時間の変動を捉えるのに向いており, 地震予知, 火山噴火予知などの研究のために重要なデータを提供している.
2-4-3-1. 水平位置を求める測地測量(**)
三角測量とは, 山頂などの見晴らしの良い所に三角点(図25)と呼ばれる測量の基準点を置き, そこから見える三角点の間の角度を精密に測る測量である. 三角測量には水平方向の角度と水平からの高度角の2つの角度が読み取れる目盛がついた望遠鏡(トランシットと呼ぶ)が用いられる. これにより, ある三角点から他の2つの三角点(この上にやぐらを組み, 遠くからでも見えるようにする)を見た方向の間の角度を測る. 原理的には3つの三角点によって作られる三角形の形は, 1辺の長さとその両端の角度がわかれば決まるが, 実際の測量には誤差があるため, 3つの角度の大きさを測る. また, 三角点の標高差も水平からの高度角の測定により求められが, 気圧や温度の変化により光が屈折するので, 三角測量によって求めた高さには, ある程度の誤差が含まれる. しかし, 他に山の標高を求めるよい方法がなく, 国土地理院の地形図に載っている山の標高は三角測量により求められたものである. なお, 三角測量は角度のみの測量であるため, スケールを求めるために基線と呼ばれる基準となる三角点間の距離を別途精密に求めておく必要がある(図26).
光波測距は, レーザー光を用いて距離を測る測量である. 三角形の辺の長さを測るので, 角度を測る三角測量に対して三辺測量とも呼ばれる. 距離を求めたい一方の観測点に図27のように測距儀を置き, 他方の観測点には反射鏡を置く. 測距儀から, 適当な周波数で変調したレーザー光を発射し, 反射鏡で反射した光を捕らえ, 発射したレーザー光との位相差を調べることにより, 距離を求める. 反射鏡には, 光が斜めにあたっても必ず入射方向に光を反射する三角錐の形をしたプリズムのコーナーキューブが用いられる. なお, 1つの波長の位相差のみでは波長の整数倍の長さを決めることができないため, レーザー光を異なる波長で変調し, それらの測定値を組み合わせて距離を測定する. 光の速度は温度, 気圧等により変化するため, 測距儀と反射鏡の位置で気象観測を行い, 光の速度の補正を行なうが, 光路の途中の気象データが手に入らないので, 完全にはこの補正ができない. そのため, 最近では長距離の測量はGPSにとってかわられるようになったが, 光波測距は, 今でも, 火山活動などの短距離の地殻変動調査や, 測角とあわせたトータルステーションとして, 建設現場の測量などに用いられている.

図25. 三角点.
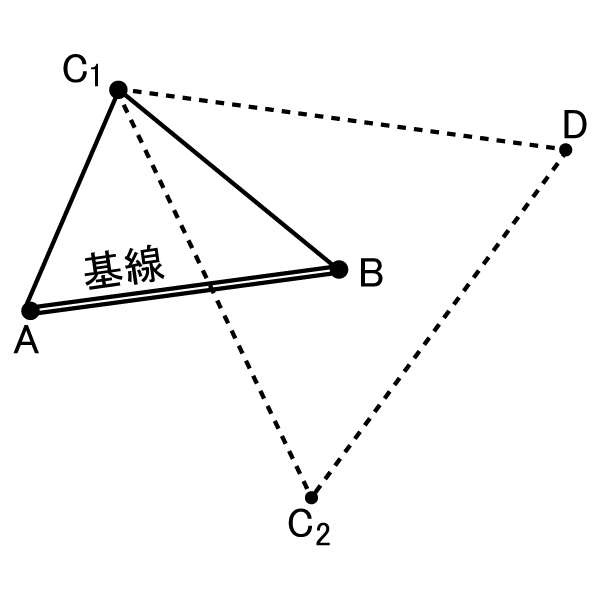
図26. 三角測量の原理. 正確に求められている基線ABを用いC1, C2の水平位置を決定し, そのC1, C2を用い, Dの水平位置を決定するというように, 順次, 三角網を広げていく.

図27. 測距儀による観測.
2-4-3-2. 高さを求める測地測量(**)
高さは, 三角測量によっても測定することが出来るが, 高さが異なる観測点間の角度測定では, 大気の屈折率の影響が大きく, 精度が悪くなる. 高い精度で高さ(標高)を求めたい場合は水準測量を行う必要がある. 高さの基準となる水準点(図28)の標高は, 水準測量により決められている.
水準測量は, 図29のように, 高さの差(比高)を知りたい2ヶ所に標尺と呼ばれる物差しを立て, その中間部に水平に置いた望遠鏡(水準儀あるいはレベルと呼ぶ)で標尺の目盛を読み取り, その差から比高を求める(図30). 1回の測定では長くても70m程度の距離の比高しか求められないため, 離れた点の比高を求めるときは尺取虫のようにこの測定を繰り返す. 日本では, 一等水準測量として通常1日に2kmの往復測定を行っており, 2kmの距離で3mm程度以下の誤差と, 非常に高精度で比高が求まる. そのため, 宇宙測地技術が多く用いられている現在でも, 精度の高い比高を求めるには水準測量が用いられている. また, 最近は標尺がバーコードとなっているディジタル・レベルも多く用いられるようになり, 瞬時に標尺の目盛りを読み取ることが可能となるなど, 水準測量も簡易化が進んでいる.
水準測量の結果として得られるものは, あくまで比高であり, 測定点間の高さの差である. そのため, 標高の基準を設ける必要があり, この基準として, 東京三宅坂の国会議事堂の向かいに水準原点が設置されており, ここの標高(24.3900m)の変化は, 三浦半島の油壷にある験潮場との間の水準測量により監視されている.
なお, 水準測量で求めた比高から正標高を計算するためには, 水準点の重力値とジオイドから水準点までの平均の重力値が必要である. このため, 国土地理院では水準点における重力測定も実施している.

図28. 一等水準点. 日本ではこのような水準点が国道に沿って約2km毎に設置されている.

図29. 水準測量. 2本の標尺の中央に水準儀を置き, 両側の標尺の目盛りを読み取る.
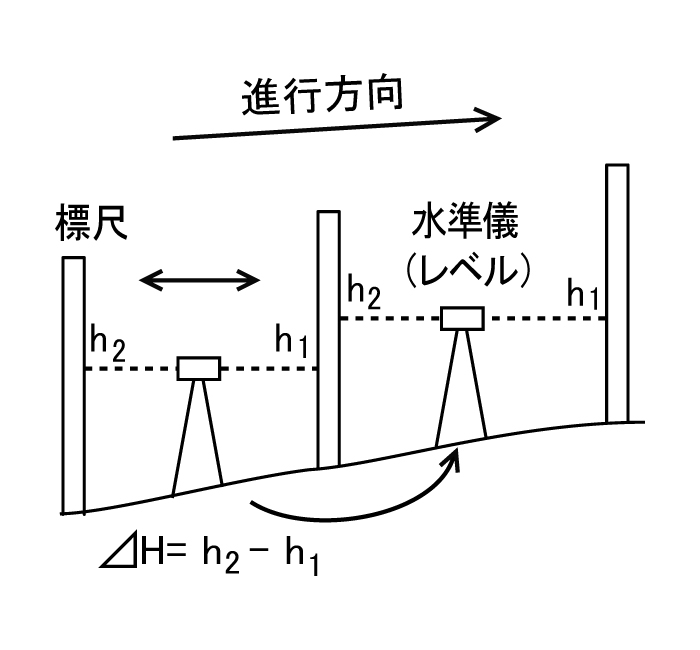
図30. 水準測量の原理. 後方の標尺の目盛り(h 2)と前方の標尺の目盛り(h 1)の差⊿ H =h 2-h 1が2点間の比高となる.
2-4-3-3. 地殻変動連続観測(**)
地殻変動連続観測では, 地面の傾斜変化を測る傾斜計, 地面の伸縮を測る伸縮計(ひずみ計), 体積変化を測る体積ひずみ計などが用いられる.
傾斜計には, 数m~数10m(数100mのこともある)離れた水槽の間を水管でつなぎ, 両端の水位を測ってその差の変動から地面の傾斜変化を求める水管傾斜計(図31), 鉛直に吊るした錘の位置の変化を測る鉛直振子式のもの, 工作物の水平を確かめるときなどに用いられる気泡管と同じ原理のバブルセンサーを用いたものなどがある. これらの計器は温度変化に弱く, それを避けるために, 通常, 水管傾斜計は地下トンネル内に設置される. また, 鉛直振子やバブルセンサーを用いたものは, 深いボーリング孔の中でボアホール傾斜計として用いられる. 以前は水平振子を用いた傾斜計もあったが, 調整が難しく不安定なため, 最近ではほとんど用いられていない.
伸縮計には, 基準尺として線膨張率の小さい溶融水晶やインバール系の合金の管を用い, その片方を地面に固定して(固定端), もう一方の端(自由端)で地面との変位を測定する水晶管(あるいはインバール管)伸縮計(図32)や, 基準尺の代わりにレーザー干渉計を用いて数10m~数100mの距離を連続的に測るレーザー伸縮計などがある. これらも温度変化を避けるため, 地下トンネル内に設置されている.
地下の体積変化を測る体積ひずみ計としては, シリコンオイルを封入した円筒に, ベローズ(蛇腹)と呼ばれる体積変化に敏感な可動部分を取り付けたものが用いられている. 円筒の体積が縮めば, 円筒中のシリコンオイルがベローズに押し出されるので, ベローズの変化を測ることにより体積変化を測定することが出来る. このような体積ひずみ計は関東, 東海地方に多く設置されており, 東海地震の予知のための重要な資料を提供している.
これらの地殻変動連続観測用の計器は, 一般にひずみに換算して10-8~10-9と非常に高い感度を持つが, 観測点が浅い場合には, 地表付近の地下水などの影響を大きく受ける. そのため, テクトニックな変動を求めるには, これらの影響をいかに取り除くかが重要である.
検潮所(験潮場)では, 図33に示すように, 観測井に導水管と呼ばれる管で海水を導き, 水面に浮かべた浮きの高さの変化で, 海面の高さを測っている. 気象庁では高潮や津波の監視, 国土地理院では平均海面の決定, 水路部では海洋潮汐の調査と水路確保を主な目的として, 観測を行っている. それぞれの観測所を, 検潮所, 験潮場, 験潮所と異なった呼び方をしているが, 実体は同じものである. 検潮(験潮)記録から地殻変動を検出するためには, 海面変動と地殻変動を分離する必要がある. このため, 地殻変動を議論する場合, 近くの検潮所では海面変動がほぼ同じであると仮定して, その水位の差を用いたり, 海面変動がほぼ同じと考えられる地域の平均値からの差を用いたりしている. 海面高の変化を測定する方法としては, 浮きの他に, 水圧計や, 超音波で水面までの距離を測る方法などがある.

図31. 水管傾斜計の水槽. 浮きを浮かべ, その高さを, 連続的に測っている.

図32. 水晶管伸縮計の自由端. 片方の端を固定し(固定端), 自由端で地面との変位を測る.
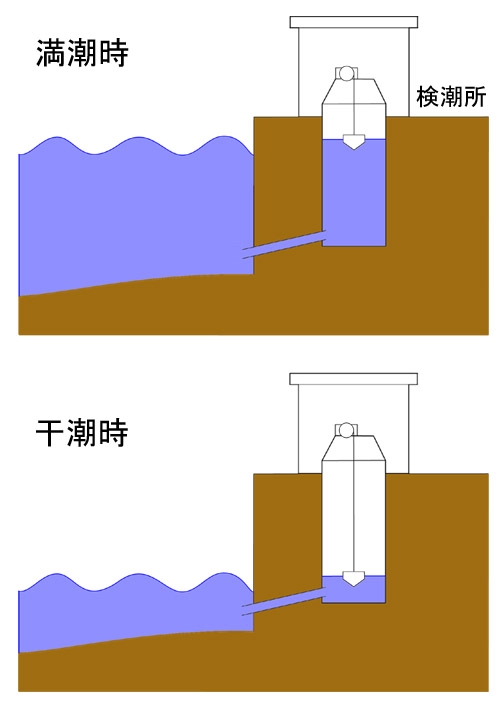
図33. 検潮所(験潮場, 験潮所)の原理.
参考文献・関連Webサイト
- 国土地理院のホームページ内「GPS」のページ
- 土屋淳・辻宏道(1991):やさしいGPS測量, 日本測量協会.
- 国土地理院のホームページ内「星が伝える大地の動き」のページ
- 高橋冨士信・近藤哲郎・高橋幸雄(1997):VLBI技術, オーム社出版局.
- 国土地理院のホームページ内「SAR」のページ
- 飯坂譲二監修(1998):合成開口レーダー画像ハンドブック, 朝倉書店.
- 鍵山恒臣編(2003):マグマダイナミクスと火山噴火, 朝倉書店.
- Fu L.L and A. Gazenave (ed.), (2001): Satellite Altimetry and Earth Sciences, Academic Press, 463p.
- Sandwell, D. T., W.H.F. Smith. (2001): Bathymetric Estimation, Chapter 12 in Satellite Altimetry and Earth Sciences, ed., L.L. Fu and A. Cazenave, Academic Press, 441-457.
- 福田洋一(2000):衛星アルティメトリィと衛星重力ミッション, 測地学会誌, 46, 53-67.
- Wide-Swath Altimeter Report
- Micro-g社のホームページ

