2-3-1. プレートテクトニクス(*)

プレートテクトニクスとは, 地球表面が多数のプレート(板状ブロック)に分かれ, プレートがほとんど変形することなく水平運動しているという主張である. その発端は1910年代にウェゲナーによって提唱された大陸移動説で, 大西洋をはさんで南北アメリカ大陸とヨーロッパ・アフリカ大陸の海岸線の凹凸が良く一致する事実と, 遠く離れた大陸間で共通する古生物分布をうまく説明する.

一般に広く受入れられなかった大陸移動説は, 1950年代に岩石の熱残留磁気測定によって復活する. 火成岩が生成時の高温状態から徐々に冷えるとき, 内部の磁性鉱物はその時代の地球磁場の方向に帯磁し, 以後はそれが固定され保存される. 同じ時代に生じた火成岩の帯磁方向から当時の地磁気の極位置を復元すると, 北米の岩石を用いた結果とヨーロッパの岩石を用いた結果が一致しない. これを説明するには, 2つの大陸が以前はつながっており, ある時期に分離して遠ざかっていったと解釈せざるを得ない.

1960年代初頭にヘスとディーツによって海底拡大説が提唱された. 大西洋中央海嶺における高い熱流量, 中軸谷を持つ地形, 引っ張り応力型の浅発地震活動などの特徴は, 海嶺の下でマントル対流が湧き上がり, 新たな海底地殻が形成され両側に移動していくことによって説明されるというものである. その直後, バインとマシューズにより, 海嶺をはさんで両側に対称的な縞状の地磁気異常(図1)の原因が解明された. 海嶺下で冷却し地殻に付加されたマントル物質が当時の地球磁場の方向に帯磁し, 海嶺の両側に移動していくことにより, 左右対称の地磁気異常が生じたと解釈できる. 岩石の年代と海嶺からの移動距離から, 年間数cmという海底の移動速度が初めて定量的に求められた.

1960年代後期に, マッケンジー, モーガン, ルピションは地震のスリップベクトルの方向, トランスフォーム断層の走向, 地磁気縞模様から推定される拡大速度などのデータを用いて地表はブロックごとに剛体運動をしていることを明らかにし, プレートという概念を導入するとともに主要なプレートの運動(図2)を決定し, ここにプレートテクトニクスの成立を見ることとなる.

図1. 北アメリカ太平洋岸沖の海底磁気異常. 出典:杉村新｢グローバルテクトニクス｣(東京大学出版会, 1987). 原図は Vine, F. J. (1968):The History of the Earth’s Crust, ed. by Phinney, Princeton Univ. Press, 73-89 より.

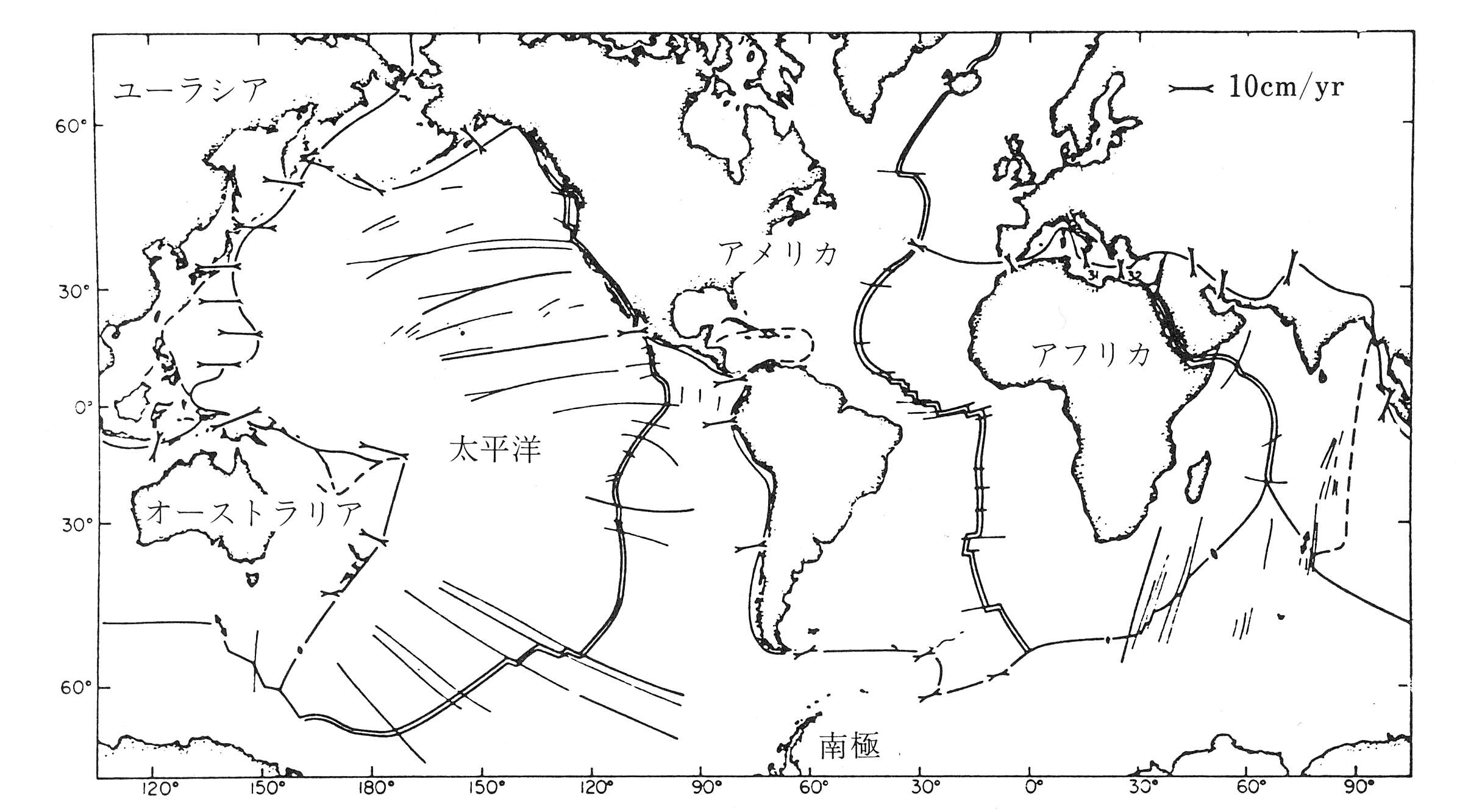
図2. 最初のグローバルなプレート相対運動モデル. 出典:瀬野徹三｢プレートテクトニクスの基礎｣(朝倉書店, 1995). 原図は Le Pichon, X.(1968):Sea-floor spreading and continental drift, J. Geophys. Res., Vol.73, 3661-3695. より.

2-3-1-1. プレートテクトニクス概観(**)

地殻-マントル-核という物質や組成の違いに基づいた区分に対し, 力学的な挙動の違いに注目すると, 地球表層部は, 数10km～100kmの厚さを持つリソスフェア(プレート)と, その下の低粘性で流動性の高いアセノスフェアとに区分される(図3).

プレート同士が接する境界は発散, 横ずれ, 収束の3つに大別できる. 発散境界(図4a)は海洋プレートが生成される場で, 一般に海嶺を形成し, 高熱流量, 張力場, 海嶺をはさみ対称的な地磁気縞模様の異常などの特徴を持つ. プレートが離れて生じた隙間を高温のアセノスフェア物質が埋める. 冷却固化しプレートに付加されたアセノスフェア物質は, 密度の増加に伴って沈降するとともに, プレートに付随して横に移動していく.

プレートの横ずれ境界(図4b)はトランスフォーム断層と呼ばれ, 発散境界や収束境界をつなぐ. トランスフォーム断層に沿って両側のプレートは互いに反対方向にずれるが, 断層に直交する方向に圧縮力は働かないので, 断層の強度は小さく, 質量の過不足は生じない. トランスフォーム断層の走向は, プレート運動の方向を直接的に示している.

収束境界は, 近づきあう2つのプレートの密度差により, 沈み込み帯と衝突帯に分けられる. 海洋プレートは大陸プレートやその下部のアセノスフェアより密度が大きく, 両者がぶつかる場所では, 海洋プレートが大陸プレートの下に沈み込む(沈み込み帯, subduction zone). 密度の大きい古い海洋プレートが, 密度の小さい若い海洋プレートの下に沈み込む場合もある. ただし, 沈み込みが開始されてからの年代, 沈み込むプレートの年齢, プレート間の相対運動速度などの違いにより, 沈み込みには異なる様式が存在する(図4c). 沈み込みの角度がゆるやかな場合, プレート同士が大きな相互作用を及ぼしあい, プレート境界に巨大地震を発生させる. また, 沈み込んだプレートがある深さに達するとマグマが形成され, その上部にプレート境界に平行な火山フロントを形成する.

大陸プレート同士がぶつかると, 密度が小さいため, どちらのプレートも他方の下に十分沈み込むことはできない. 結果として物質の集中が起こり, 厚い地殻を形成する(衝突帯:collision zone). ヒマラヤ山脈はインドプレートとユーラシアプレートの衝突の結果生じたものである.

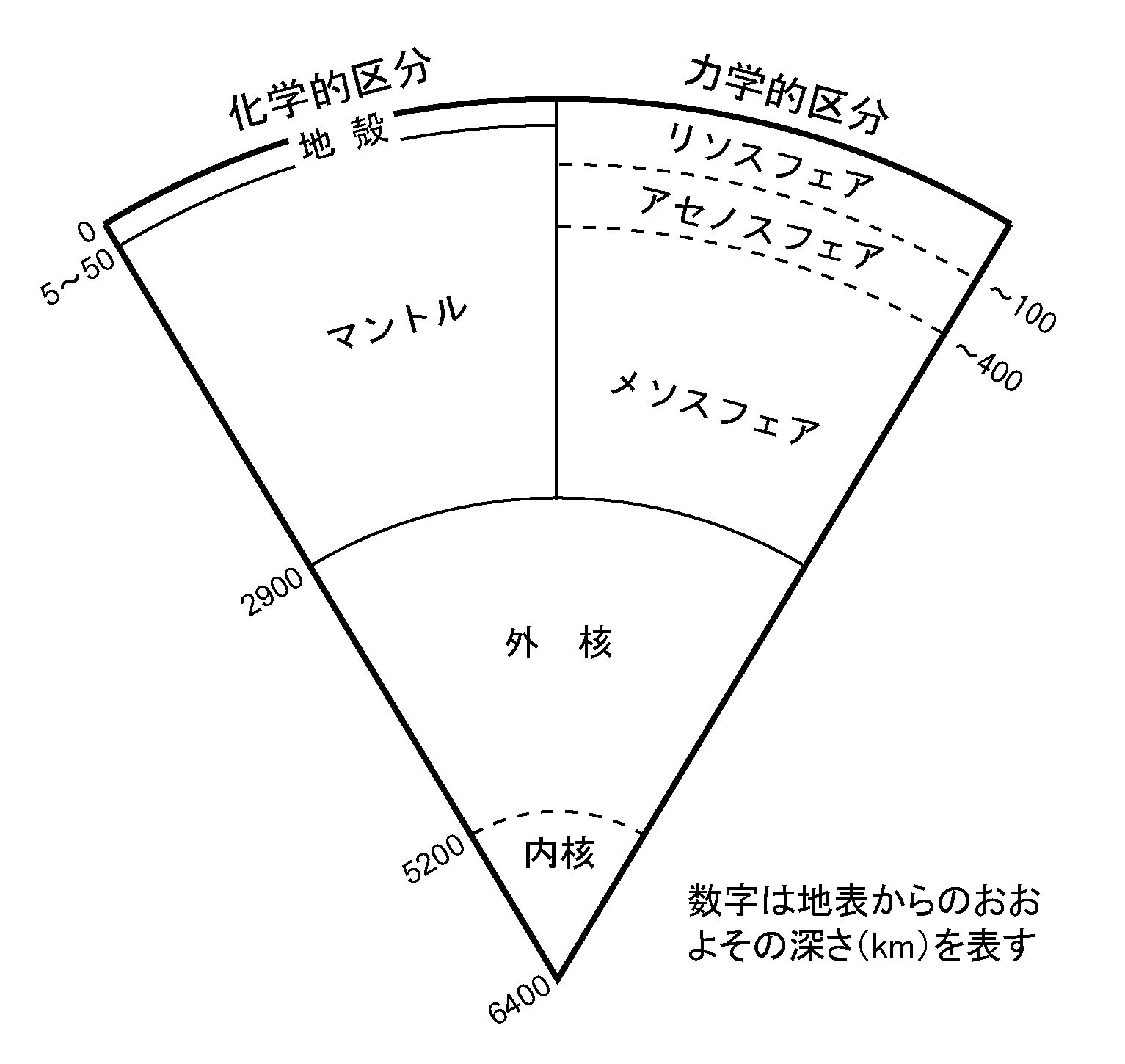
図3. 地球内部の層区分. 構成物質や化学組成の違いに基づいた化学的区分と, 外力に対する応答に基づいた力学的区分とは一致しない.

図4a. プレートの発散境界.

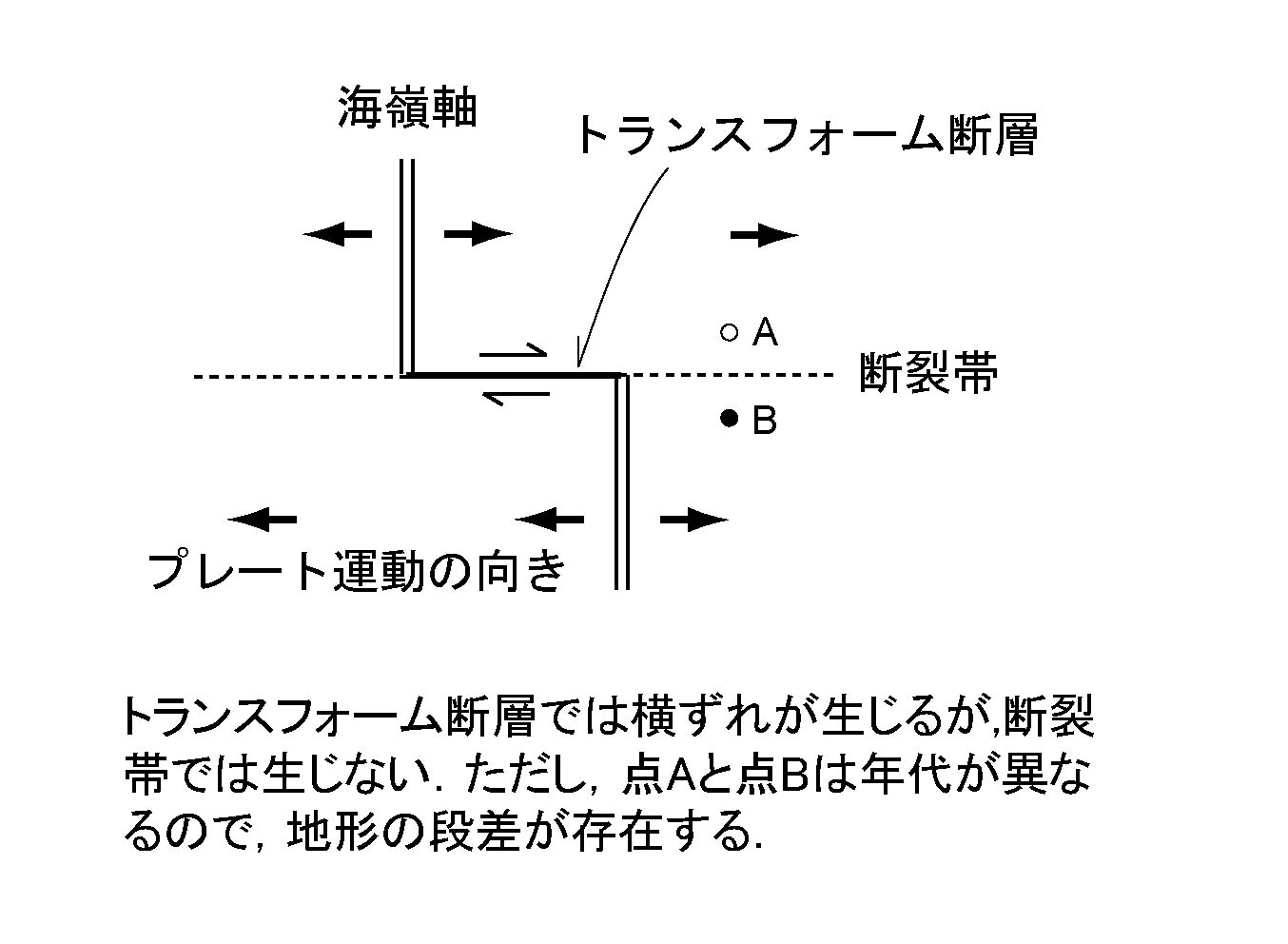
図4b. プレートの横ずれ境界.

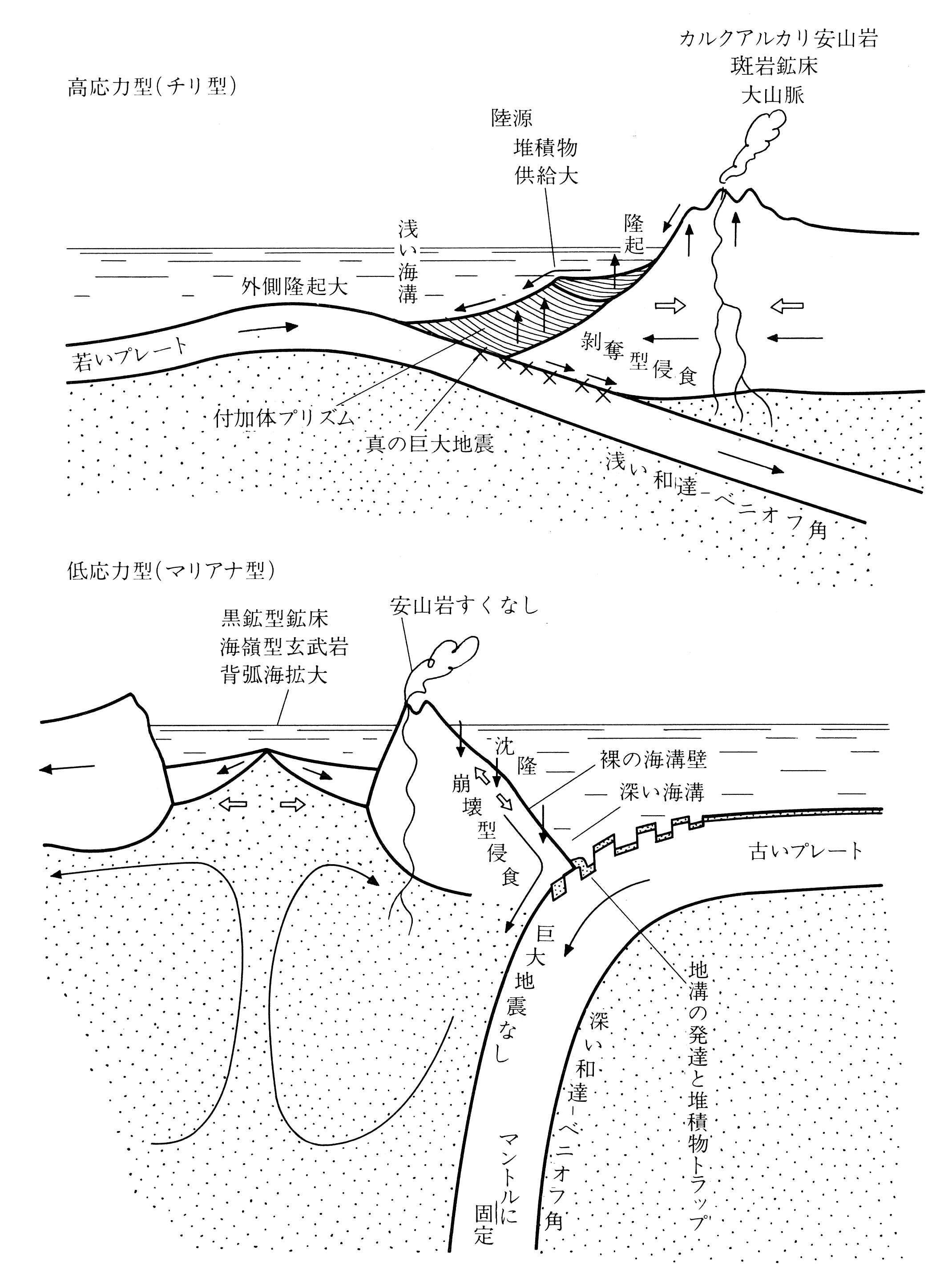
図4c. 2つのタイプのプレート収束境界. 出典:上田誠也｢プレートテクトニクス｣(岩波書店, 1989). 原図は Uyeda, S.(1984):Subduction Zones: Their diversity, mechanism and human impacts, GeoJournal, Vol.8, 381-406. より.

2-3-1-2. プレートテクトニクスの検証(**)

1980年代後半まで, プレート運動を決定する際には, 海嶺の拡大速度やトランスフォーム断層の走向といった地質データと, 収束境界に発生する地震のずれの向きと量(スリップベクトル)が用いられてきた. 地質データは過去数十万年から数百万年間の平均的なプレート運動を与えるが, 現在もその運動が引き続いて進行しているかどうかの保証はない. 一方, 地震データは現在のプレート運動を反映したものであるが, スリップベクトルの方向がプレートの真の運動方向を表しているか, また, プレート運動のどれだけの割合が地震の発生に費やされているか, などの点に不確実性を含んでいる.

1980年代中頃から宇宙測地技術が急速に発展し, プレート運動の直接的な実測が可能となった. VLBI観測は, 日本に対しハワイが6.3cm/yrの速さで近づいていること(図5a, 大西洋をはさんだ北米とヨーロッパが1.7cm/yrの速さで遠ざかっていること(図5b), などを明らかにした. これらの結果は, 地質データと地震データから決定されたプレート運動モデルが予測する値と良く一致する. SLR観測結果も同様である. すなわち, 現在進行中のプレート運動は, 少なくとも過去数十万年間の長期にわたり, 安定していることを示している. こうして, 1990年までに, プレート運動は観測事実として完全に認知された.

1990年代に入るとGPS観測が広く普及し, VLBIとSLRに比べ観測点数は大幅に増加した. この結果, プレート運動をさらに詳細に決定することが可能となった. プレート運動モデルとの比較だけでなく, 現在では, プレート内部の変形様式も活発に議論されている.

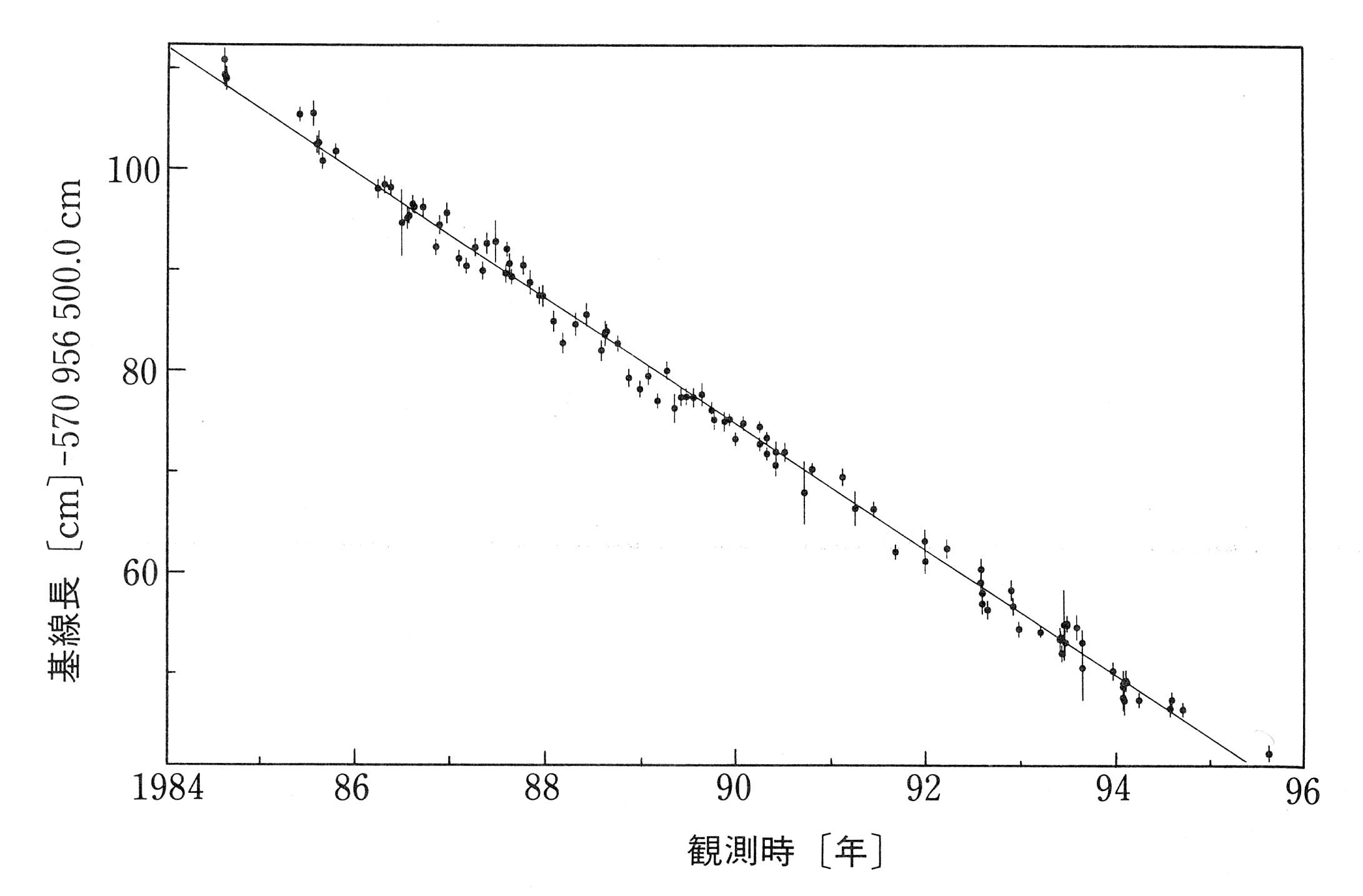
図5a. 茨城県鹿嶋市とハワイとの間の距離変化. 鹿島34mアンテナとハワイ9mアンテナとの間のVLBI観測結果を示す. 出典:高橋富士信・近藤哲郎・高橋幸雄｢VLBI技術｣(オーム社出版局, 1997).

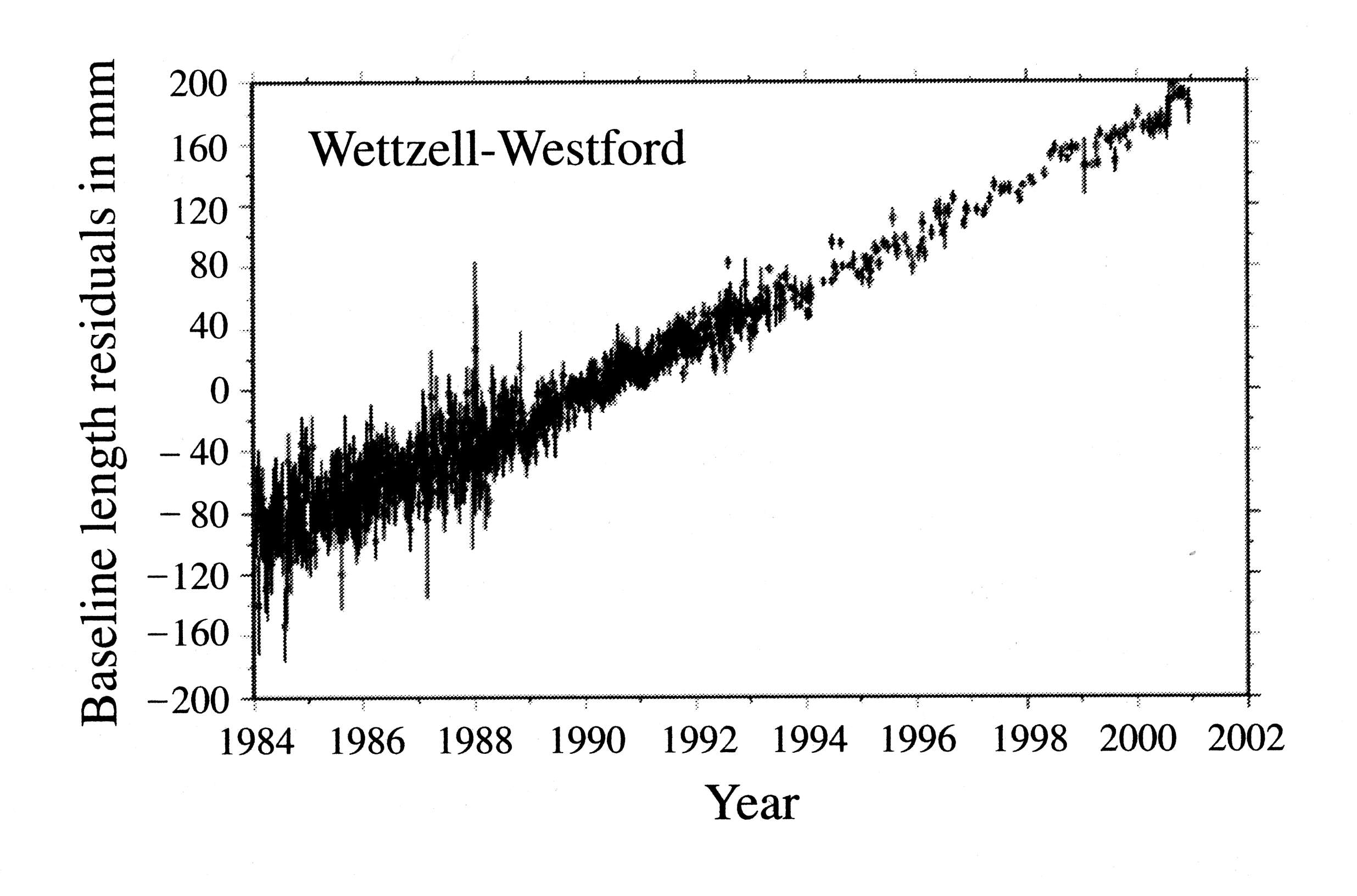
図5b. 大西洋をはさみ6000km離れたWettzell(ドイツ)とWestford(米国)との間の距離変化. 出典:Seeber, G., “Satellite Geodesy (2nd edition)”, Walter de Gruyter, 2003.

2-3-1-3. プレート運動の表現(***)

プレート運動のように地球表面に沿った水平運動は, ｢オイラーの定理｣(第4部付録)により, 地球の中心を通るある1つの軸の回りの回転運動として表現できる(図6). 回転軸と地表の交点2ケ所のうち, 上から見下ろしたときプレートが反時計回りに回転する方の交点を, 回転極(オイラー極)とする.

測地学や地震学が扱う時間スケールでは, プレートが移動した累積距離よりも, 現在の運動速度の方が重要である. しかし, プレート運動の速度は高々数cm/yrであり, 短い時間スケールの移動量は地球半径に比べ無視できるほど小さい. このような回転は“瞬間的”な無限小回転(第4部付録)として扱うことができる. すなわち, プレート運動を記述するパラメーターは, 回転極の緯度, 経度および軸回りの角速度の3つである. また, 地球の中心から回転極の方向を向き, 角速度と同じ大きさを持つ回転ベクトル(角速度ベクトル, オイラーベクトル)も, プレート運動の表現に用いられる(図7).

無限小回転の特徴は, 回転ベクトルの足し算が可能なことである. 3つのプレートA, B, Cの間の相対運動を考えたとき, Bに対するAの回転ベクトルとCに対するBの回転ベクトルが既知であるとすると, 両者の和は, Cに対するAの回転ベクトルを与える. 結果は足し算の順序によらない. 実測データによってプレート間の相対運動を直接決定できない場合でも, 周辺のプレートの運動がわかれば間接的に予測することが可能である.

地質学的時間スケールでは, プレートが移動した累積距離が問題となる. このとき, プレート運動は回転極の位置と回転角の大きさで表される. 地球半径に比べて移動距離が無視できなければ, もはや無限小回転として扱うことはできない. このような有限回転では, 回転の足し算の可換性は成立しない. プレートBに対するAの有限回転とプレートCに対するBの有限回転が既知であるとき, どちらの回転を先に行うかで, 回転の足し算結果は異なる. 遠い過去のプレートの位置を復元する際には注意が必要である.

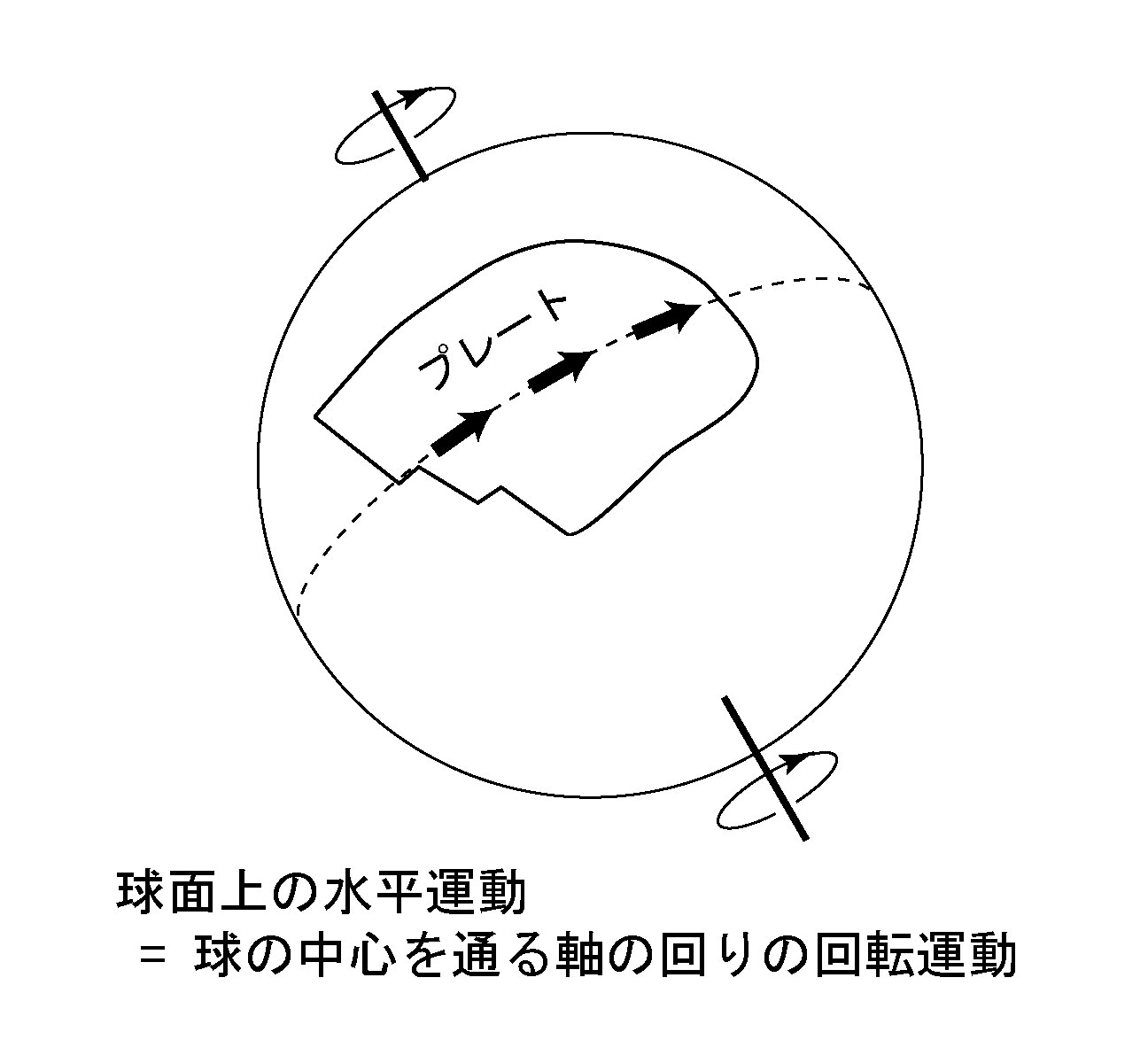
図6. 球面上の水平運動. 球の中心を通る1つの軸の回りの回転運動として表現できる. 軸が球面と交わる位置および軸まわりの回転角(あるいは角速度)によって表される.

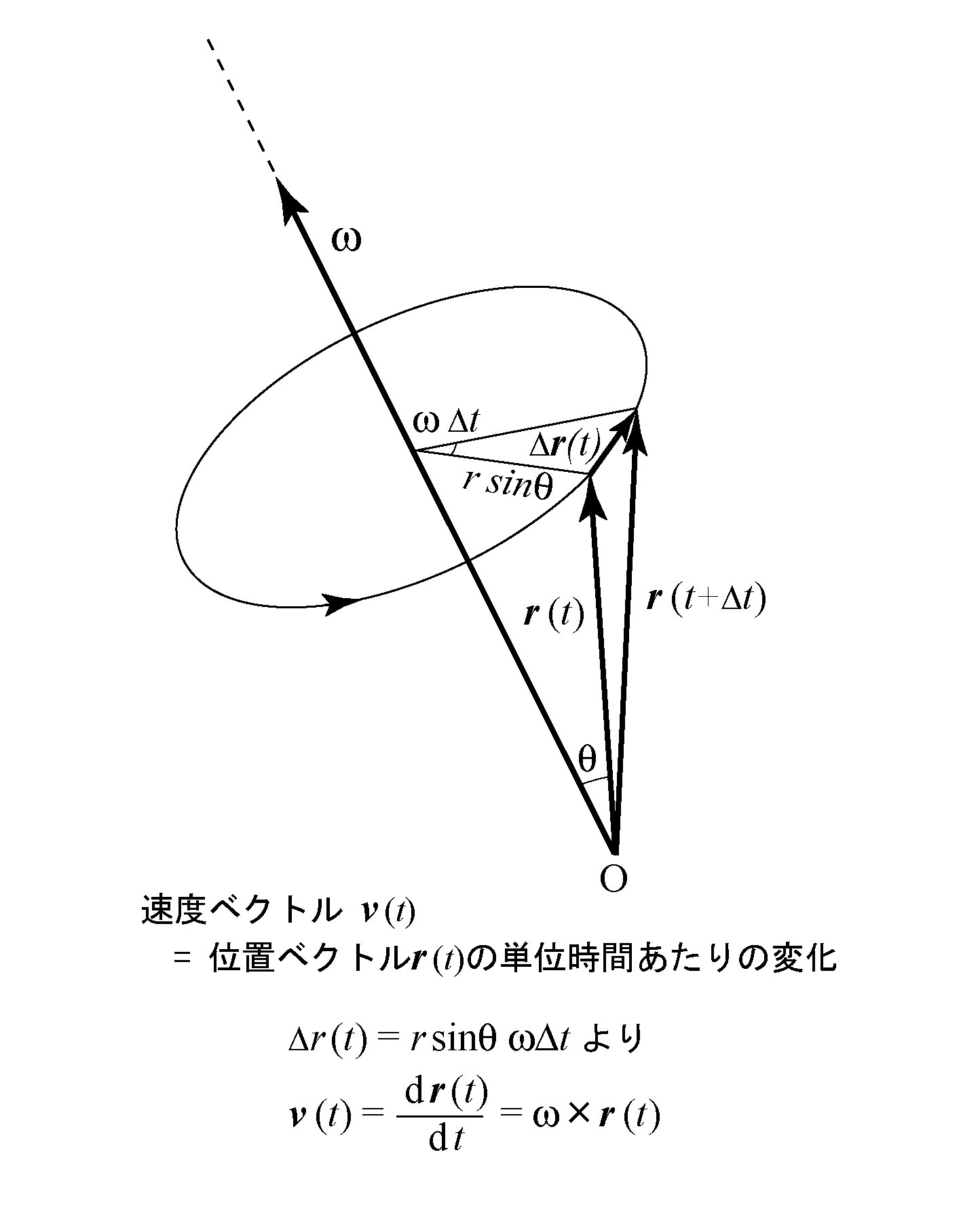
図7. 回転ベクトル(角速度ベクトル), 質点の位置ベクトル, 質点の速度の関係.

2-3-1-4. プレートの相対運動と絶対運動(***)

海嶺の拡大速度, トランスフォーム断層の走向, 地震のスリップベクトルの方向, 異なるプレートに属する2点間の距離変化などは, 2つのプレート間の相対的な運動に関する情報を与える. 常に, どのプレートに対する運動かに注意する必要がある. 一方, すべてのプレート間の相対運動関係を保ったまま, 地球に固定された基準座標系に対する運動に変換されたものが, プレートの絶対運動である(図8). 地球上のすべての観測点はプレート運動によって移動しており, 絶対運動を求めるには何らかの別の基準が必要である.

ハワイに代表されるホットスポットは, マントル深部から上昇してその上を通過するプレートに火山の痕跡を残す. ホットスポットの位置を不動の基準としてプレートの絶対運動を記述するものが, ホットスポット基準系である. 一方, 1つのプレートの運動は隣り合うプレートの運動と作用・反作用の関係にあり, 全てのプレートの運動の総和(平均回転)がゼロになると仮定することは合理的である. 平均回転がゼロになるように調整されたものは, 平均リソスフェア(No-net-rotation:NNR)系と呼ばれる. ホットスポットのような特別な固定点を設定する必要がないが, プレートの厚さや密度が必ずしも一定ではないために, 平均回転の計算に任意性が含まれている.

2つのプレート間の相対的な回転運動の極位置と角速度をまとめた相対運動モデルのうち, NUVEL-1(Northwestern University Velocity Model 1)は, 最も代表的なものである. これに, プレートの平均回転がゼロになるよう調整を施した絶対運動モデルはNNR-NUVEL1と呼ばれている. これらのモデルの発表後に地磁気逆転年代表の改訂があり, 海嶺の拡大速度も見直しが必要となった. これを考慮して再計算されたものがNNR-NUVEL1Aで, 以前よりプレート速度は平均して4.4%ほど減少した. 宇宙測地学で利用されるITRF(International Terrestrial Reference Frame, 国際地球基準座標系)も, プレート運動に関してはNNR-NUVEL1Aに準拠している. 近年, 純粋に宇宙測地観測のみに基づいたREVEL-2000(Recent Velocity 2000)というプレートモデルも提唱されている.

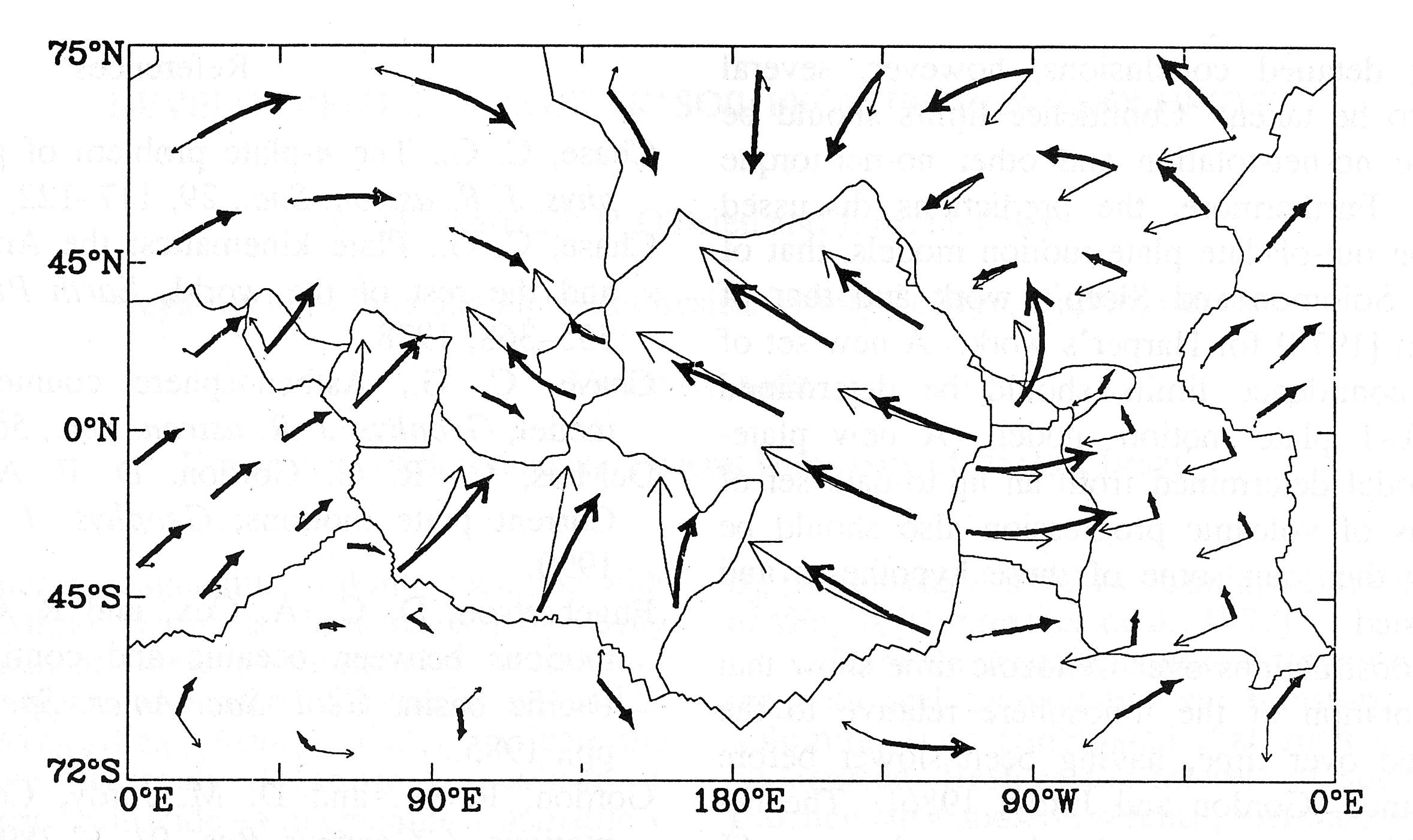
図8. プレートの絶対運動モデル. 相対運動モデルNUVEL-1を平均リソスフェア系に基づく絶対運動に変換したもの(太い矢印)と, ホットスポット系に基づいて変換したもの(細い矢印). 中央の大きなプレートが太平洋プレートを表す. 出典:Argus and Gordon(1991):No-net-rotation model of current plate velocities incorporating plate motion model NUVEL-1, Geopys. Res. Lett., Vol.18, No.11, 2039-2042.

2-3-2. 地殻変動(*)

地表にはさまざまな周期の変動が見られる. 例えば, 地震が発生すると, 周期が0.1秒以下のものから数十秒の範囲にまでわたる振動が発生するし, 普段でも数Hzから数秒程度の周期の雑微動や常時微動と呼ばれる振動がある. また, 大地震が発生したときには, 数分から数十分の周期の地球自由振動が発生する. これは弱いながらも常時生じていることが分かっている. さらに, 数時間から数日さらには1年にまでわたる周期の変形として, 地球潮汐がある. 他にも, 気圧, 海水準や地下水位の変動に伴う地表の変形も見られる.

これら周期的な変動に対して, 人間のライフタイムのスケールでは, 累積的な変形として見られる変動もある. 例えば, プレート運動に伴う地表の変形, 地震や火山活動により永久変位として残る変動などである. これらの変動を一般的に地殻変動と呼ぶが, 地球潮汐より長い周期の地表の周期的変形も地殻変動に含めることもある. これらの変動のうち, 短周期の変動については, 弾性変形として取り扱うことによりその原因を求めることができるが, 長期的な変動については粘性も考慮に入れる必要がある.

地殻変動の中には,地球潮汐のようにその原因が明らかなものもあるが, 地震や火山活動による変動のような場合は, 観測された地殻変動から, その原因としての断層運動やマグマの動き求めることになる. 断層運動やマグマの動きなどの原因が与えられたとき, 結果としてどのような地殻変動が起こるかを求めるのではなく, この場合は, 結果としての地殻変動が分かったときにその原因を求めることになる. このような問題を「逆問題」と呼ぶ.

地殻変動の研究は, 測地学的手法, 地質学的手法, 地形学的手法, 考古学的手法など, さまざまな方法が用いられるが, 100～200年より最近の変動については, 通常測地学的手法が用いられる. そのため, 地殻変動の研究は測地学の重要な研究分野の1つとなっている.

2-3-2-1. 日本列島の定常的な地殻変動(**)

日本列島は4つのプレート(太平洋プレート, フィリピン海プレート, 北アメリカプレートまたはオホーツクプレート, ユーラシアプレートまたはアムールプレート)の境界域に位置し, 活発な地殻変動がみられる. 図9に, 国土地理院のGEONETによる観測結果から見積もられた, 2001年10月から2002年10月までの1年間の水平変位ベクトルを示す. 北海道から四国にかけての広い範囲にわたり, 太平洋岸が内陸側へ圧縮されている様子がよく分かる. また, 上下変動では, 太平洋岸の多くの岬において沈降がみられ, これらは, 太平洋プレートやフィリピン海プレートの沈み込みにより, 陸側プレートが引きずり込まれているためであると解釈されている. プレート境界で大規模地震が発生したときに, これらの地域では, 逆に, 隆起および海側への水平変動が見られる. しかし, 北海道東部は, このような地震時の跳ねかえりの現象があまり見られず, 長期的に沈降の傾向を示している.

日本列島の大部分は, 太平洋プレートの沈み込みによると見られる東西圧縮の変動を示している. また, 変位こそ小さいが, 新潟付近から神戸付近にかけて, 中部, 近畿地方を縦断する地域でのひずみの蓄積が顕著に見られる.

一方, 九州から沖縄にかけては, 南東方向への変位が見られる. 南西諸島の南東への変位は, フィリピン海プレートの沈み込みに伴う陸側でのアセノスフェアの対流運動により, 東シナ海の沖縄トラフが拡大しているためであると考えられる.

図9. 国土地理院のGEONETによる2001年10月から2002年10月までの日本各地の1年間の水平変位ベクトル. 新潟県西部の上越市大潟区を不動と仮定している. (国土地理院GEONETグループ, 測地学会誌50, 53-65, 2004)

2-3-2-2. 地震に伴う地殻変動(**)

地震は急激な断層運動により発生する. 地下で生じた断層面のずれにより, 地表では地殻変動が生じる. 震源が浅い場合には断層が地表に現れることがあり, これを地震断層と呼ぶ. 最近では1995年兵庫県南部地震の際に淡路島に現れた野島断層が有名である.

断層を挟む両側の岩体の動きにより, 断層は縦ずれと横ずれの2つに分けられる. 縦ずれの場合, 断層の傾斜と両側の上下変動のパターンにより正断層と逆断層に大別される.

地下で断層が動いたときの地表での地殻変動は, モデル計算で求めることができる. これはたとえば大きな消しゴム(弾性体)に切り口を入れ, 強制的に切り口の両面をずらしたとき, 全体がどう変形するかを求めるようなものである. このような計算には, 岡田(1992)がまとめたモデルがよく使用される.

縦ずれ断層の近傍では, 上向きに動いた側に隆起, 下向きに動いた側に沈降が見られるが, 断層から離れたところでは逆向きの変動が現れることがある. とくに断層の傾斜角が小さいときにその傾向が著しい. 逆断層が動いたときの断層からの距離と変位の関係を図10に示す.

横ずれ断層の場合は, 図11に示すように主として水平方向の地殻変動が生じるが, 岩盤が引き寄せられるところに隆起, 発散するところに沈降といった上下変動も伴う.

断層モデルで実際の地殻変動が見事に説明された例として, 1923年関東地震の際の地殻変動を図12に示す. 傾斜角30^\circの右横ずれ成分を持つ逆断層による地殻変動として, 地震に伴う地殻変動が, 上下成分, 水平成分ともによく説明できている.

このような変動は, ゆっくりした断層の動きによっても生じる. 実際, 地殻変動連続観測の記録やGPSの記録から, 多くのサイレント地震(サイレントアースクエイク)やプレート間のゆっくりすべりなどが発見されている. また, 最近は地殻変動連続観測による変動と深部長周期微動との関係も注目されている.

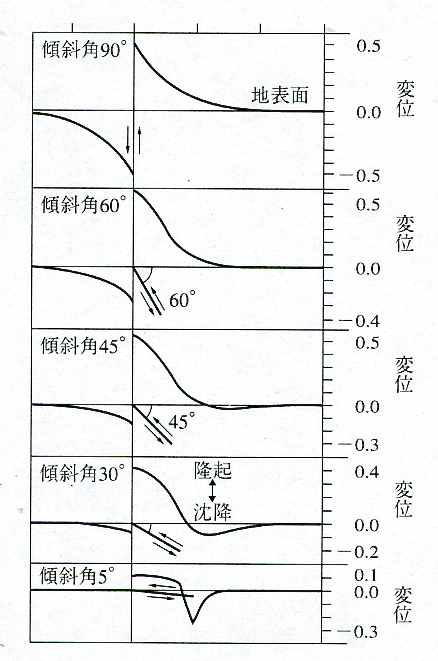
図10. 逆断層が動いたときの地表の上下変位. 縦軸の変位値は断層の変位を基準としたもの. (地学団体研究会編, 新版地学教育講座2『地震と火山』(1996)による)

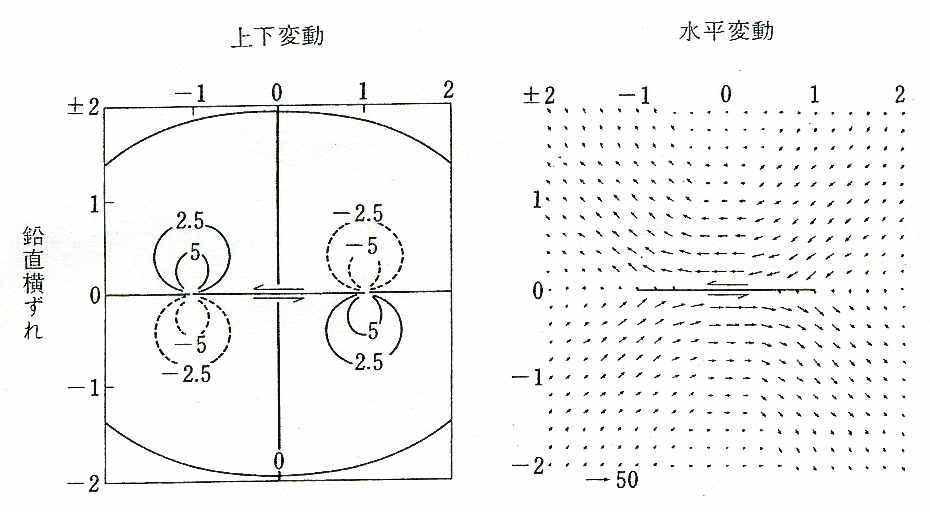
図11. 横ずれ断層が動いたときの地表の変位. 断層の長さ2, 幅1, 上端の深さ1/15の場合で, 断層の変位が1mのときのcm単位の地表の変動. (原図:松浦・佐藤, 1975, 宇津徳治『地震学第3版』(2001)による)

図12. 1923年関東地震のときの水平変動と垂直変動. (a)は実測値で, A-Bは地震の断層の位置を表す. (b)は, 長さ85km, 幅55km, 右横ずれ成分6m, 逆断層成分3m, 傾斜角30^circの断層がモデルから求められる地殻変動. (原図:安藤1973, 地学団体研究会編, 新版地学教育講座2『地震と火山』(1996)による)

2-3-2-3. 火山活動に伴う地殻変動(**)

火山活動では地下でマグマが動く. マグマが地下深部から上昇してきてマグマ溜りの圧力が上昇するとその周辺は同心円状に隆起し, 逆にマグマがなくなって圧力が下がると沈降する. マグマの動きによる地盤の隆起・沈降や水平変動のパターンは, 火山活動の活発な地域を中心に, ほぼ同心円状に見られる. 地下で球状の圧力源の変化があったときの地殻変動は茂木モデル(茂木, 1958)により計算できる. それによると, 圧力源が浅いほど変動の範囲が狭く, 深いほど広くなる. 従って, マグマの上昇に伴う圧力変化で地殻変動が生じたとすると, 地殻変動からマグマの深さを推測することができる.

従来から, 多くの活火山に傾斜計やひずみ計が設置され, 地殻変動観測による火山活動の監視が続けられてきたが, 最近ではGPSによる地殻変動観測が盛んに行われている. GPSで観測された火山活動による地殻変動の例として, 2000年3月の有珠山の噴火前後の地殻変動の様子を, 3月29日から31日までの半日毎の水平変動で示す(図13). 噴火を開始したのが31日の13時7分であるので, 噴火の1～2日前に山体が大きく膨張していることがわかる.

GPSや地殻変動連続観測では, 地上に観測計器を設置した地点での変動が求まるが, 地殻変動を空間的に連続的に捉えることはできない. 一方, 干渉SARを用いると, 火山周辺の地殻変動パターンを平面的に連続に捉えることができる. 実際, 干渉SARにより, 岩手山, 三宅島などの活動に伴う地殻変動がきれいに得られている.

図13. GPS観測によって捉えられた2000年3月有珠山の噴火に先立つ地殻水平変動. 噴火開始は3月31日13時7分である. (高橋裕晃・他, 火山47巻161-166(2002)による)

2-3-2-4. 地殻変動に伴う重力変化(**)

重力は, 地球潮汐や気圧変化, あるいは, 地下水やマグマなどの地下質量の移動以外にも, 地殻変動による測定点の位置の変化によっても時間的に変化する. 地殻変動による重力変化は, 地下の質量移動による変化と地表, つまり観測点の移動による変化が合わさったものである.

地下で密度$\rho$の物質が移動し, その分だけ地表の高さが変化したとすると, そのときの重力変化$\Delta g$と高さ変化$\Delta h$の関係は, 地下で密度$\rho$の物質が移動し, それの分だけ地表の高さが変化したとすると, そのときの重力変化$\Delta g$(mGal)と高さ変化$\Delta h$ (m)の関係は,

\[ \frac{\Delta g}{\Delta h} = -0.3086 + 2 \pi G\rho \tag{1} \]

図14に愛知県十四山村での地下水くみ上げによる地盤沈下に伴う重力変化の例を示す. 1978年までは, くみ上げられた水の体積分だけ地盤が沈下しているが(Wの線), それ以降は地下水くみ上げ規制により沈下の停止とともに水が戻ってきたことによる重力の増加が見られる.

ただし, 地下にマグマ溜りなどの大きな空洞があり, そこにマグマが出入りしたような場合は, 隆起でも重力が増加したり, 沈降でも重力が減少したりする場合もある.

地下で断層が動いた場合, 地表の上下変動ばかりではなく地下の密度変化も生じる. この場合の重力変化は大久保(1992)により求められている.

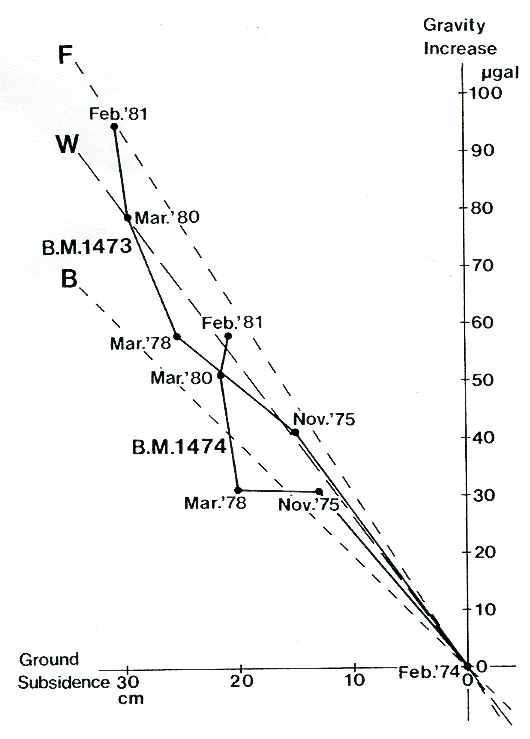
図14. 地盤沈下にともなう重力変化の例. Fはフリーエア勾配, Bはブーゲー勾配, Wは水が増減した分だけ隆起沈降を起こす場合の重力と高さ変化の関係を示す. (Satomura M., Geosci.Repts.Shizuoka Univ. 11, 1-55, 1985)

2-3-3. 地球潮汐(*)

潮汐というと, 一般には海面が1日に2回上下する潮の満ち干, すなわち海洋潮汐のことを思い浮かべるであろうが, 固体の地球も, 海洋潮汐と同じように弾性変形を起こしている. この固体地球が潮汐変形する現象を地球潮汐と呼ぶ.

潮汐を起こす力, つまり起潮力は, 月や太陽など地球外の天体の引力が基となっている. 地球上の各地点に働く引力は, 地球に大きさがあるために天体からの距離に差が生じることで, 場所によりわずかに異なっている. 一方, 慣性系から見ると，地球と天体とは, その引力によりそれぞれが並進加速度運動を行っている. 地球が太陽の周りを1年に1回公転しているのも, 月が地球の周りを1ヶ月に1回公転しているのも, この並進加速度運動であり, より正確には, いずれも共通重心の周りの運動である. ところで, 地球に固定された並進座標系から見ると，この並進加速度運動による慣性力は, 地球のすべての点で同じであり, この慣性力とつりあった天体の引力と, 地球上の位置でわずかに異なる天体の引力との間に差が生じる. この差が起潮力である(図15).

地球潮汐とは, 天体の起潮力によって引き起こされる固体地球の変形(ひずみ, 傾斜, 伸縮など)や重力変化などの総称であり, 例えば, 重力の変化は重力潮汐, ひずみの変化はひずみ潮汐などと呼び, 区別することもある.

もし, 地球が完全な剛体であれば, 起潮力によりポテンシャルが変化することによる重力や傾斜変化は存在するものの, 地球の幾何学的な形状そのものが変化することはない. しかし, 実際の地球は, 完全な剛体ではなく, 弾性的な性質や粘弾性的な性質を持つために, 起潮力により, 幾何学的な形状そのものも変化する. 天体の引力に由来する起潮力は, 大変正確に計算することができる. 従って, 起潮力によって変形した地球を観測することで, 地球の弾性的性質, あるいは, 粘弾性的性質を知ることができる. 地球潮汐の観測では, 重力計, 傾斜計, 伸縮計, ひずみ計などが用いられるが, これらのデータを組み合わせることで, ラブ数, 志田数とよばれる起潮力に対する地球の変形の度合いをあらわす定数を求めることができる.

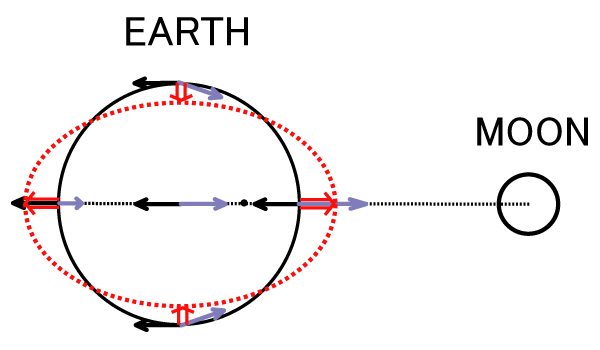
図15. 起潮力は, 天体の引力による並進加速度運動（共通重心(O)の周りの公転等)による慣性力(黒ベクトル)と, 天体による引力(青ベクトル)の差(赤ベクトル)として計算される. 並進加速度運動による慣性力は地球上のどこでも等しく(そして, 地球の重心に働く天体の引力に一致する), 天体の引力は場所によって変化する. その結果, 図の赤い点線のような起潮力の分布になる.

2-3-3-1. 分潮(**)

起潮力は, 基本的に天体の引力を起源とするので, 公転に伴う地球と天体との距離の変化や, 地球の自転に伴う観測点と天体との位置関係の変化などにより時間的に規則正しく変化する. これらの変化は, 例えば, 平均太陽日($15^\circ/hour$)や平均太陰日($14.492^\circ/hour$)のように決まった周期を持っており, 起潮力もこのようなさまざまな周期を持つ正弦波の和として表すことができる. これら1つ1つの正弦波を地球潮汐の分潮と呼び, 特に振幅の大きなものは主要分潮とよばれている.

潮汐の各分潮は, 周期が約12時間の半日周潮, 約1日の日周潮, それより長周期の長周期潮に大別される. これらは, それぞれ扇球(Sectorial)潮, 方球(Tesseral)潮, 帯球(Zonal)潮と呼ばれることもあるが, これらの呼称は, 起潮力ポテンシャルを導く際の, それぞれに対応した2次の球面調和関数に由来している(第4部付録参照, 図16).

半日周潮の代表的なものとしては, 周期が12時間25分のM2分潮, 12時間のS2分潮, 12時間39分のN2分潮が, 日周潮としては, 周期が23時間56分のK1分潮, 25時間49分のO1分潮が, また長周期潮としては, 月の公転に伴う13.66日周期のMf分潮, 27.32日周期のMm分潮や, 地球の公転による半年周期のSsa分潮, 1年周期のSa分潮がある. 中緯度に位置する日本では, M2分潮の振幅が大きく, 1日に2回の潮の満ち干がはっきりしているのもこのためである.

主要分潮の一覧表を第4部付録に示す.

図16. 扇球項, 方球項, 帯球項の起潮力分布のイメージ. 上からそれぞれ, 半日周潮, 日周潮, 長周期潮を表している.

2-3-3-2. ラブ数, 志田数(**)

もし地球が剛体であれば起潮力が働いても変形しないが, 現実の地球はほぼ弾性体の球と考えられるので, 起潮力によって変形する. その変形を上下方向(地球の半径方向)の$u_r$と, 南北, 東西方向(水平方向)の$u_\phi$ , $u_\lambda$に分けて考えると, 起潮力ポテンシャルを$U$, 地球の重力を$g$として,

\[ \begin{equation} \begin{array}{l} u_r=\frac{h}{g}U \\ u_\phi=\frac{l}{g}\frac{\partial U}{\partial \phi} \\ u_\lambda=\frac{l}{g\cos\phi}\frac{\partial U}{\partial \lambda} \end{array} \end{equation} \tag{2} \]

で与えられる. また, このような地球の変形が生じると, そのために地球の内部での質量の再配置が起こり, 地球の重力ポテンシャルも変化する. その変化分$V$は起潮力ポテンシャル$U$に比例し,

\[ V=kU \tag{3} \]

で与えられる. ここで, $h, l,k$は, 起潮力に対する地球の変形を表す定数で, ラブ(A. E. H. Love, 1863–1940)によって導入された$h, k$をラブ数(Love's numbers), 志田順(1876–1936)によって導入された$l$ を志田数(Shida's number)と呼ぶ. 現実の地球では, ラブ数, 志田数は, それぞれ, $h =0.61-0.62, k =0.30-0.31, l =0.08-0.09$程度の値をとる.

次に, 起潮力ポテンシャル$U$が働いた場合の重力ポテンシャル$W$の変化$\Delta W$を考えてみよう. 弾性変形の結果, 観測点は$u_r$だけ上下変動を起こすために$-u_r \cdot g =-h \cdot U$ のポテンシャル変化が生じることを考慮すると

\[ \Delta W=U+V-u_r \cdot g =(1+k-h)U=\gamma U \tag{4} \]

となる. ここで, $\gamma=(1+k-h)$は減少定数とよばれ, 0.6～0.7程度の値をとる.

地球潮汐による重力変化の場合には, $\delta$定数とよばれる同様の減少定数

\[ \delta=1-\frac{3}{2}k+h \tag{5} \]

が存在し, その値は, 1.16程度となる.

もし地球が完全な弾性体であれば, これらの値は場所や周期に依存せず一定の値となる. しかし, 現実の地球では, 流体核による共鳴効果などにより, これらの値が周波数依存性を持つことが知られている. 現在の地球潮汐観測は, 弾性体理論からのδ 定数の僅かな違いなどから, 地球の深部構造や粘弾性的な性質を探ることが主要な目的となっている.

(注) 重力潮汐を表す$\delta$定数

\[ \delta=1-\frac{3}{2}k+h \tag{5} \]

のうち, 第1項は起潮ポテンシャルによる直接の影響を, 第2項は地球の弾性変形に伴う地下の質量再配分によって重力ポテンシャルが変化することによる重力変化を, 第3項は弾性変形に伴う観測点の位置変化による重力変化をそれぞれ表している.

2-3-4. 地球回転(*)

地球回転とは, 地球の自転のことであるが, 一見, 非常に安定なように思われる地球回転もさまざまな要因で変化している.

地球回転には3種類の異なった変動がある. 第一に, 歳差・章動と呼ばれる地球の自転軸が宇宙空間に対して変動する現象, 次に, 極運動と呼ばれる自転軸に対して固体地球が変動する現象, そして最後に, LOD(Length of Day)変動と呼ばれる自転速度が変動(1日の長さが変化)する現象である.

歳差・章動は, 地球回転をコマの回転にたとえると, コマの軸が空間に対して動く現象で, その原因は, 地球潮汐と同じく月や太陽の引力にあり, 公転面に対して傾いた地球の赤道上での天体の引力の差が自転軸を起こそうとする偶力として働くことによる. 歳差と章動とはいずれもこの偶力の結果であり, 起源は同じで, 月や太陽の軌道の変化にさまざまな周期成分があることから, 歳差運動中の小振幅で周期の早い変化成分を章動と呼んでいる.

極運動とは, コマの形状軸と実際の回転軸が僅かにずれた出来の悪いコマのように, 各瞬間の自転軸が地球の形状軸(慣性モーメントが最大となる軸)のまわりを回転する運動のことである. 歳差・章動は自転軸の方向, すなわち天の北極の方向が変化する現象であるが, 極運動は, 地球上での自転軸の位置の変化であり, 観測点の天文経緯度の変化として観測される. 特に, 緯度変化は恒星の位置観測で検出されるので, かつては極運動観測のための国際的な共同観測事業が展開されていた. 現在, これらの観測は, VLBIなどの宇宙測地観測に引き継がれている.

歳差・章動の原因は天体の起潮力であるが, 極運動, あるいはLOD変動の主な原因は地球そのものにある. 短期的なLOD変動の原因の大部分は, 大気と固体地球との間の角運動量の交換(すなわち風が自転速度を変化させること)によることが知られているが, 最近の研究では, 極運動のひとつである周期約430日のチャンドラー極運動(チャンドラーウォブル)も, 大気や海洋の変動に起因すると考えられるようになっている.

2-3-4-1. 歳差, 章動(**)

地球の形状は完全な球ではなく, 赤道方向に膨らんだ回転楕円体に非常に近い. また, 地球の赤道面は黄道面(地球の公転軌道面)に対して約$23.4^\circ$傾いている. このため, 膨らんだ赤道部分に働く太陽の引力(起潮力)を考えると, 図17に示すように, 地球の自転軸を起こそうとする偶力(トルク)が働くことになる. 自転している地球に対してこの偶力が働くと, 地球の自転軸も, コマの首振り運動と同じような, 自転の向きと逆行する運動を引き起こす. これが歳差である.

月の公転軌道である白道は, 黄道面に対して, $5.9^\circ$傾いているが, 月の引力による歳差も太陽の引力による歳差と同様に働き, これらを加えたものを日月歳差と呼ぶ. 日月歳差により, 地球の自転軸, すなわち天の北極は, 地球の公転軌道面つまり黄道に対して約$23^\circ26'$の傾きを保ったまま, 自転の向きとは逆の向きに約25800年の周期で回転している. 現在はこぐま座のアルファ星がほぼ天の北極にあり, 北極星と呼ばれているが, 歳差のために天の北極の位置はどんどん移動し, 12000年後には, こと座のベガが北極星になる(図18).

地球の公転軌道は円軌道ではなく, ほぼ楕円軌道であり, 月の公転軌道も同様に楕円軌道である. さらに, それぞれの軌道はさまざまな周期で変化している. 従って, 月や太陽の引力で地球を起こそうとする偶力の大きさも, さまざまな周期で変化することになる. このため, 地球の自転軸は, 約25800年の周期の歳差だけではなく, 小振幅のさまざまな周期の変動が重なることとなる. これらの運動を章動と呼び, 振幅が最大ののものは, 周期が約18.6年で, その振幅は約9''程度である. これは, 黄道と白道との交点(月の昇交点)が黄道上を約18.6年で逆行する現象に関連している. こうした歳差・章動は, 月や太陽の引力が偶力として働く必要があり, 図16から想像できるように, 日周潮汐(Tesseralモード)と対をなすものである.

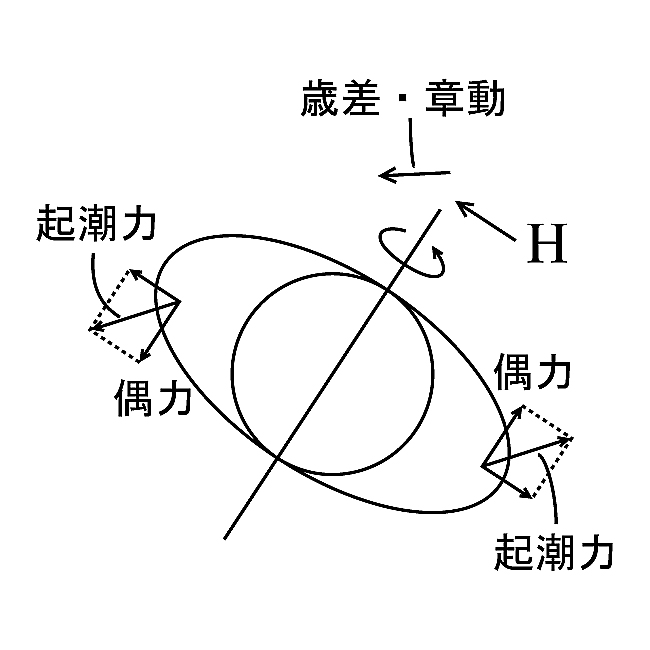
図17. 起潮力と歳差, 章動.

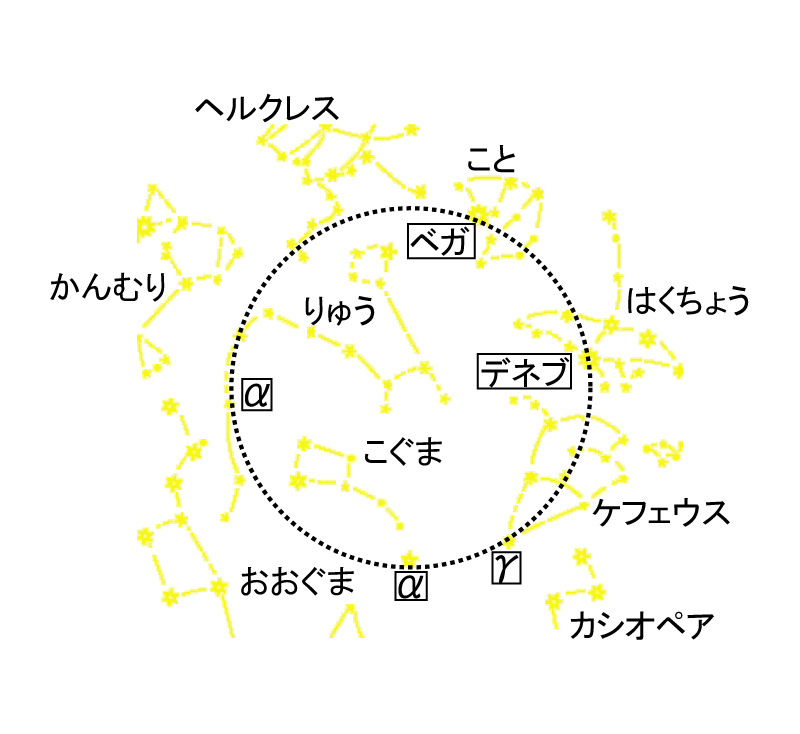
図18. 歳差による北極星の移り変わり. 現在は, こぐま座のアルファ星が北極星であるが, 2000年後にはケフェウス座のガンマ星, 8000年後にははくちょう座のデネブ, 12000年後にはこと座のベガ, 21000年後にはりゅう座のアルファ星と移っていく. こぐま座のアルファ星が再び北極星となるのは, 約25800年後である.

2-3-4-2. 極運動と木村のZ項(**)

地球の自転軸が宇宙空間に対して変動する現象が歳差・章動であったが, 極運動は, 固体地球に対して自転軸が変動する現象であり, 地球の形状軸と瞬間の自転軸とがずれている場合に生じる.

極運動は一種の自由振動で, 回転楕円体の瞬間自転軸は, 外力がない場合には, 形状軸のまわりを, 周期

\[ T=\frac{2\pi A}{\omega (C-A)} \tag{6} \]

19世紀末, チャンドラーはおよそ430日の周期で地球が半径数mの極運動していることを発見した. この極運動はチャンドラー極運動(チャンドラーウォブル)と呼ばれ, その周期は, 地球が剛体ではなく弾性的な振舞いをするためにオイラー周期が伸びたもので, チャンドラー周期と呼ばれる.

極運動により, 地球の極がある方向にずれると, ずれた方の観測点では緯度が高くなり, 反対の観測点では緯度が低くなる. 従って, 極運動を詳しく調べるためには, 経度の異なる観測点で緯度の変化を同時に精密に観測すればよい. このような目的で, 1899年に国際緯度観測事業が開始され, 世界各地の5ヶ所の観測所と共に, 岩手県の水沢に臨時緯度観測所が設置された.

今, 形状軸からの極(瞬間自転軸)のずれを$x,y$で表すと, 経度$\lambda$の観測点での緯度の変化$\Delta \phi$は, 図19に示すように,

\[ \Delta \phi = x\cos\lambda + y\sin\lambda \tag{7} \]

\[ \Delta\phi=x\cos\lambda + y\sin\lambda + z \tag{8} \]

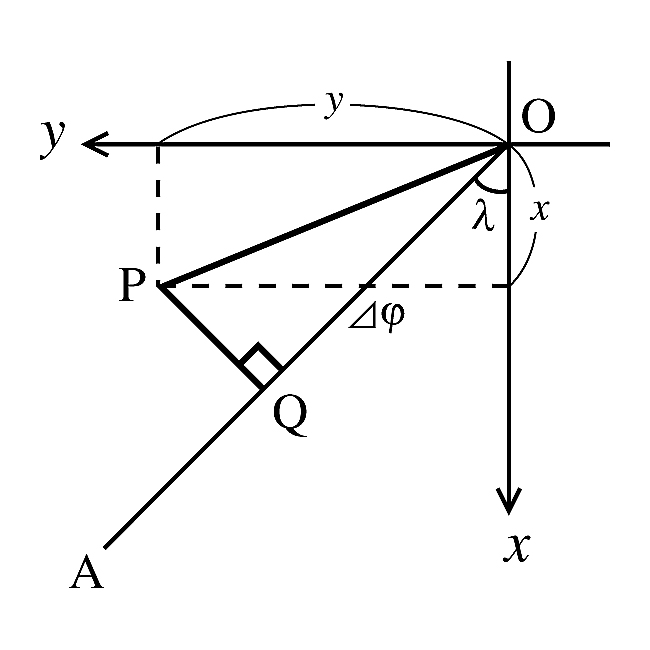
図19. 極運動の座標系.

(注) 1970年代になり, 同じく水沢緯度観測所の若生康二郎によって, Z項の原因が, 地球が流体核を持つことによる自由核章動(Free Core Nutation)にあることが突き止められた.

2-3-4-3. 自転速度の変化(**)

一般に, 閉じた系では, その系内の角運動量(角速度と慣性モーメントの積)の総和は変化しないという角運動量保存則が成り立つ. これを地球の場合にあてはめると, 自転による角運動量を含め, 地球での角運動量の総和が一定であることを意味する. 地球の持つ角運動量の大部分は, 固体地球(より正確にはマントル)の自転による角運動量であるが, そのほかに地球表面をとりまく大気も, 貿易風や偏西風のように固体地球とは独立に運動できるので, 固有の角運動量を持っている. これらの風の変化による大気の角運動量の変化は, 地表面での摩擦をとおして固体地球との角運動量の交換が起こり, 結果として地球の自転速度に変化をもたらす.

自転速度の変化によるLODの変化は, ミリ秒(1/1000秒)のオーダーであるが, 1980年台以降, VLBIをはじめとする宇宙測地技術を利用して観測されるようになった. また, 大気の持つ角運動量については客観解析データを利用した計算が可能となり, 両者を比較することにより, 現在, 数年より早い周期の自転速度変化の原因は, その大部分が大気によることが確かめられている.

一方, 数十年周期の変動については, まだ不明な点が多いが, その原因として, 長周期の気候変動などとともに, 地球磁場変動との関係も指摘されている. 地球が流体核を持つことを考えると, 流体核とマントル間での角運動量のやり取りがあっても不思議ではなく, 地球深部構造を知る上で大変興味深い研究テーマである.

以上は, 地球を閉じた系と考えた場合であるが, 実際には潮汐現象をとおして, 地球－月の系での角運動量の交換も行われている. 地球の自転エネルギーが海洋潮汐摩擦により消費されると, 地球自転の角運動量が減少することになるが, この減少した角運動量は月の公転運動の角運動量に移動する. そのため, 地球の自転速度は僅かずつ遅くなり, 月は地球から遠ざかる永年運動を行っている.

現在は, 時刻の基準を原子時計で決めているので, 地球の自転速度が変化すると, 原子時計で決められた時刻と地球の自転運動とがあわなくなってくる. そのため, 原子時計の時刻と地球の自転との差が0.9秒を超えると1秒入れることになっており, この1秒をうるう秒と呼ぶ. また, このようにして決まられた世界時を協定世界時と呼び, UTCと記す. 協定世界時より9時間進めたものが日本標準時である.