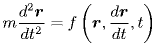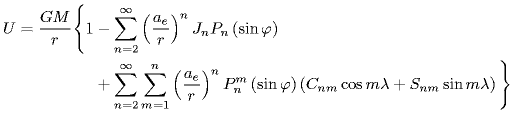SLRをはじめとする人工衛星を用いたグローバルな測地には，当然ながら衛星の正確な軌道が必要不可欠である．

　人工衛星の運動は，衛星の運動方程式を解くことによって知ることができる．

　ここで，m は衛星の質量，r は衛星の地心位置ベクトル，f (r ,d r /d t ,t )は衛星に働く力をそれぞれ表している．運動方程式は2階の常微分方程式であるから，衛星に働く力がわかれば，上式を数値的に解くことによって衛星の運動を知ることができる．

　人工衛星の軌道はどのようなものであろうか．

　地球の重力ポテンシャルは，球面調和関数で展開することができる．

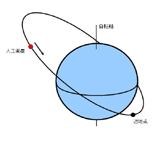
　ただし，G は重力定数，M は地球の質量，a _eは地球の赤道半径，r は衛星の地心距離，φ は衛星の緯度，λ は衛星の経度である．地球の重力は，第一次近似として，地球の質量全体が重心に集まった質点からの引力と見なすことができる（主要項：G M /r ）．この場合，運動方程式は良く知られているように二体問題に帰着し，衛星の軌道はケプラー運動（楕円軌道）となる（図6）．主要項の次に大きいのがJ ₂を含む項である．J ₂項は，衛星の軌道半径にもよるが，概ね主要項の約1/1000の大きさになり，その他の項の大きさはさらにその1/1000以下のオーダーになる．

　衛星の軌道高度が高くなると，地球の重力ポテンシャルの高次項の影響を受けにくくなる．例えば，月くらい離れてしまうと，もはや地球を質点と見なして差し支えない．しかし，衛星の軌道が低い場合は地球の重力場の短波長成分の影響を強く受け，軌道を正確に計算するには地球の重力ポテンシャルの高次項まで考慮する必要が生じる．

　人工衛星に働く力としては，この他，月・太陽の潮汐力による地球の変形に起因する重力変化，海洋潮汐による重力変化，月・太陽の潮汐力，太陽光の輻射圧，地球からの輻射圧，大気抵抗力，衛星表面からの熱輻射による反動など様々なものがある．重力以外の力は衛星の面積に比例するため，表面力と呼ぶことがある．表面力は衛星の自転軸や衛星表面の光学的・熱的性質に依存する．

　SLRの解析では，衛星に働く力から衛星の軌道を求めるとともに，歳差，章動，地球回転，伝播遅延，潮汐や荷重変形による観測点の変位などをモデル化して，衛星までの距離を算出し，観測された距離と比較する．現在では，観測精度が向上したため，相対論的な効果も考慮されている．実際の解析プログラムでは，膨大なSLRデータを解析処理することにより，衛星の軌道とともに地球の重力場，観測局の座標，地球回転パラメータなどの物理パラメータを推定する．一般に，パラメータはある程度真値に近い値がわかっているものとして，観測方程式を線形化し，最小二乗法によりパラメータを推定する（Montenbruck and Gill, 2000, Sanso and Rummel, 1989）．