|
地球変動であるチャンドラー極運動の励起源の調査は,地球全体の角運動量保存則に従う.つまり,地球システムを構成するマントル,コア,海洋,大気,陸水・雪氷圏の角運動量の総和は,時間変化しないことから,地球全体の角運動量収支を見ればよい.コア・マントル非結合によりマントルとコアは独立と見なせ,その角運動量は観測された極運動(図1参照)の微分で計算できる.一方,大気や海洋等の角運動量は,大循環モデルの出力から求める.大気大循環モデルの場合,数値予報という現業で使用されているため,現実の大気状態に近づけるべく気象観測値が同化される.この過程で得られる6時間毎の3次元格子データである全球客観解析値(最近では再解析値)から大気角運動量が計算され,大気・マントル間の角運動量収支の研究に用いられてきた(国際地球回転事業のSpecial Bureau for the Atmosphere,IERS/SBAでも公開されている).チャンドラー極運動の励起源としても大気変動がすぐに注目され,1970-1980年代においては気圧変動による大気質量再配分効果が論じられたが,観測されたチャンドラー極運動の励起の20-30%程度しか説明できなかった.ところが近年になって,衛星観測データが同化され精度が格段に向上したことにより,それまで励起を論ずるに足る精度が得られなかった風による相対角運動量成分が,14ヶ月周期近傍でパワーを持ち,観測されたチャンドラー極運動を励起するのに十分な角運動量を持つことが発見された(Furuya et al. 1996, 1997; Aoyama and Naito, 2001).これらの日本発の研究は気象庁データに基づく大気角運動量を用いてなされたが,奇妙な(不幸な?)ことにIERS/SBAで公開されている米国環境予測センター(NCEP)のデータから計算された風の相対角運動量には,同様なピークは見当たらず,チャンドラー極運動を励起するパワーも足りなかった(Gross, 2000; Aoyama and Naito, 2001).ところがNCEP再解析値から角運動量を計算しなおすと,図3に示す通り,風の相対角運動量の14ヶ月周期近傍でピークが現れた.加えて,国際的に最も信頼されている欧州中期予報センター(ECMWF)に基づく風の相対角運動量では14ヶ月周期近傍に顕著なピークが認められた.さらに気圧の寄与を加えると,観測されたチャンドラー極運動を励起するのに十分なパワーを持つことが示された(Aoyama et al., 2003).風の相対角運動量は時間とともに変動するが,少なくとも,1980-1993年の期間は風(特に対流圏の風)が最も主要なチャンドラー極運動の励起源であると考えてよいことが分かる. 風の約14ヶ月周期の変動の存在は,Gross氏の「チャンドラー極運動の励起において海底圧力変動が重要である」という主張と相容れないものではない.なぜなら海洋角運動量の計算に使用される海洋大循環モデルは大気角運動量の計算にも使用されている再解析値の風(ならびに熱フラックス,そして最近は気圧も)で駆動されているからである.Gross氏は明言していないが,海洋にも14ヶ月周期変動が存在する.例えば,以前より海水面変動データの解析から,北海での非常に振幅が大きい極潮汐(極潮汐はチャンドラー極運動による地球の重力変化に対する海洋の応答で,14ヶ月周期を持つ)が報告されており,それは風の吹き寄せに起因すると説明されている(Tsimplis et al., 1994; O'Connor et al., 2000).加えて,風の14ヶ月周期現象は赤道域の太平洋に見られる14ヶ月近傍の海洋変動(Naito, 1983; Philander et al. 1989; Jin et al. 2003)などとも関係がある可能性が高い.今後,海洋大循環モデル(あるいは駆動力となる大気再解析値)が高精度になることで,海洋角運動量にも前述したような14ヶ月周期近傍にピークが出現することは十分考えられる. こうなると,大気・海洋の14-16ヶ月周期変動がチャンドラー極運動を励起するという考え方(例えば,Plag, 1997が提唱)が現実味を帯びてくる.これまでチャンドラー極運動の励起といえばランダム変動が暗黙のうちに仮定されてきたが,14-16ヶ月周期変動が発見されることで,チャンドラー極運動のダイナミクスそのものも再考する必要があるかもしれない.少なくともマントルの非弾性を反映するQ値も変わってくるであろう.14-16ヶ月変動が大気・海洋のどのような地球変動によるものであるのか,またマントルの長周期帯における物性構造の解明など,チャンドラー極運動の問題はまだまだ課題の尽きない分野横断型の研究テーマである. |
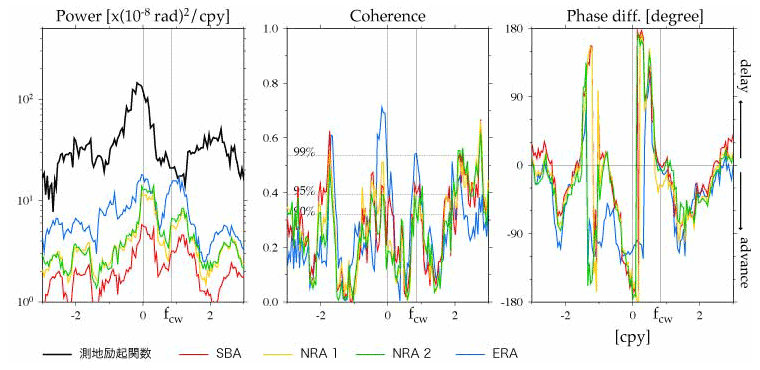
図3.1980-1993年に観測された極運動角運動量(測地励起関数)と風による相対角運動量効果のスペクトラム解析結果.右からパワースペクトル,測地励起関数と風による相対角運動量効果のコヒーレンスと位相差.SBAはSBAで公開されているNCEP/NCAR再解析値に基づく大気角運動量,NRA 1は NCEP/NCAR再解析値,NRA2はNCEP/DOE AMIP II再解析値,ERAはECMWFの再解析値に基づく大気角運動量(NCEP/DOE AMIP II再解析値はNCEP/NCAR再解析値のバグ修正版の位置づけ).SBAとNRA1は同じ再解析値に基づくが,相対角運動量効果を計算する際に,SBAは地形を考慮せず NRA1は地形を考慮し鉛直積分を行っている.この単純な計算方法の違いにより,SBAには山脈の内部に吹く偽の風の寄与が含まれ,両者のスペクトル解析結果に大きな差が生じる(詳細はAoyama and Naito, 2000). 参考文献 Aoyama, Y. and I. Naito(2000):J. Geophys. Res., 105, 12417-12431. Aoyama, Y. and I. Naito(2001):J. Geophys. Res., 106, 8941-8954. Aoyama, Y. et al.(2003):Earth Planets and Space, 55, e25-e28. Furuya, M. et al.(1996):J. Geophys. Res., 101, 25537-25546. Furuya, M. et al.(1997):J. Phys. Earth, 45, 177-188. Gross, R. S.(2000):Geophys. Res. Lett., 27, 2329-2332. Jin, F. F., et al.(2003):Geophys. Res. Lett., 30(2), doi:10.1029/2002GL015983. Naito, I.(1983):Marine Geodesy, 7, 345-358. O'Connor, W. P., et al.(2000):Geophys. J. Int., 142, 620-630. Philander, S. G. H., et al.(1989):Phil. Trans. R. Soc. Long. A., 329, 167-178. Tsimplis, M. N. et al.(1994):Geophys. Res. Lett., 21, 449-452. Plag, H-P.(1997):Chandler wobble and pole tide in relation to interannual atmosphere-ocean dynamics, in "Tidal Phenomena", Lecture Notes in Earth Sciences, 66, edited by H. Wilhelm, W. Zurn, and H.-G. Wenzel, pp.183-218, Springer, Berlin. |