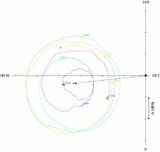
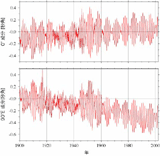
地球の自転運動は，常に一定であるかのように日常的には感じてしまう．しかし近現代の測地技術による高精度な観測によって，いろいろな時間スケールで様々な種類の変動をしていることが見えてきた．地球の回転運動が変動するという事実それ自体が科学的に興味深いだけでなく，これを高精度に観測することは地球の姿勢の決定そのものであり，人工衛星の高精度軌道決定や座標系の精密決定のために実用的にも重要である．

　地球回転変動と一口にいってもいろいろな現象があり，それぞれに名前が付いている．ここでは特に「極運動（polar motion, wobble）」，そのなかでも最も顕著な現象である「チャンドラー極運動（Chandler wobble）」に注目する．極運動とは，北極付近で地表を貫く自転角速度ベクトルの変動の軌跡を表している．図1に示すように1998年頃には○の位置に瞬間的な地球の自転軸があった．しかし2000年には△の位置で自転軸は地表を貫く，といった具合に極の位置が動くのである．直径にして3〜10mくらいの振幅をもつ．この運動を東経0°と90°成分に分け，時系列で示したのが図2である．ただちに気付くことは，6年間で「うなり」を示すことである．

　「6年間のうなり」の観測事実を地球物理学的に解釈する方法は無数にある．しかし最も単純で今日でも受け入れられている理論は，1年周期と1.2年周期の2つの主要な成分が含まれるというものである．1年周期は地球表層の大気水圏における季節変化に伴う質量分布変化や角運動量変化による一種の「強制振動」であり，一方，1.2年周期（約435日）は地球システムの力学的な特性を反映した「固有周期」であって，何らかの外力で励起されなければ観測されない「自由振動」である，と解釈する．回転楕円体に「自由振動」が存在することはEulerによって歴史的に予言されていた．その固有周期の計算はLandau and LifshitzやGoldsteinの力学の教科書にもあるとおりで，地球の形状で決まる値を用いると，この固有周期はおよそ10ヶ月（306日）になる．18，19世紀に多くの先人によってこの10ヶ月周期の極運動の検出が試みられたが見つけることができず，S.C.Chandlerによって最初に見つけられたのが14ヶ月周期の極運動であったというわけで，チャンドラー極運動と呼ばれる.

　回転楕円体の自由振動として，いつかどこかで見たことのある運動といえば一様運動を乱された直後のコマの運動がそれである．ある一様な角速度でコマを回す．きれいに回り続けるコマの縁を一瞬だけ，コツンとたたくとどうなるか．最初に与えた角速度で回り続けると同時に，ゆっくりとした「みそすり運動」を始めるのを観察できるだろう．このみそすり運動に相当するのが自由振動であり，地球の場合のそれがチャンドラー極運動である．