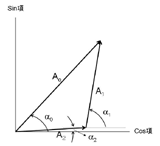
傾斜計，ひずみ計，そして重力計で観測される地球潮汐には，本来の月・太陽の引力による潮汐の他に海洋荷重による影響が含まれている．通常，前者は直接項，後者は間接項と呼ばれている．これらは，固体潮汐（Body tide or Solid Earth tide），海洋荷重潮汐（Oceanic loading tide）とも呼ばれる．

　直接項が潮汐力に対する地球の応答係数であるラブ数h ,k ,また志田数l で表されるように，荷重潮汐も同様の係数を使って表現でき，これらの係数はラブ数，志田数に対応して，荷重ラブ数h' ,k' ,荷重志田数l' と呼ばれる．荷重ラブ数h' ,k' はそれぞれ半径方向の変形のし易さ，地球の重力ポテンシャルの変化に関係した係数で，志田数l' は水平方向の変形のし易さに関係した係数である．具体的には，間接項は，地球の表面点荷重に対する応答関数（グリーン関数,h' ,k' ,l' を使って表現できる）と海洋潮汐による海水の質量分布の変化量との積を全海洋表面にわたって積分（たたみ込み積分）することで計算することができる（Farrell, 1972）．

　観測が海岸近くで行われる場合，間接項が直接項より大きくなる場合がある．例えば，北極スバルバード諸島のニーオルセンでは，海岸から約100mの位置で超伝導重力計による観測が行われているが，ここで観測されるM ₂分潮の場合，直接項の振幅が3.2μGalに対し，間接項が4.5μGalと，間接項が約1.4倍大きい（Sato et al., 2001）．

　地球潮汐を精密に観測する目的の1つに，地球流体核による共鳴現象の周期，減衰係数を精密に決め，マントル・流体核の境界で起こっている結合過程の物理を調べることがある．これには，間接項を補正した直接項の振幅を0.1%程度の精度で決める必要がある．この例でも分かるように，地球潮汐観測から地球のダイナミックスを研究する上で，間接項を精密に決めることが重要である．

　TOPEX/Poseidon衛星海面高度計データの利用が可能になり，海洋潮汐モデルの精度が飛躍的に向上した．これにより，10年程前に比べ，間接項の計算精度は大幅に改良された．国立天文台の松本らが開発した海洋潮汐モデルNAO.99bを使った荷重潮汐計算プログラムGOTIC2が国立天文台水沢観測所のWebで公開されている（http://www.miz.nao.ac.jp/staffs/nao99/index.html）．

　図1は，観測値，直接項，間接項の関係をベクトルで表した図で，フェーザプロットと呼ばれている．ここでA ₀，α ₀，A ₁，α ₁，またA ₂，α ₂はそれぞれ観測値，間接項（海洋荷重潮汐），直接項の振幅と位相を表している．

　重力潮汐の場合，ひずみ潮汐等と比べ局所的な影響が大変に小さいこと，また，地球のマントルの平均粘性率が大きい（約10^21〜22Pas）ことを反映し，間接項を補正して得られる直接項の位相α ₂は，通常0.1°以下の小さな値を示す．