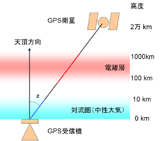
GPS測量では，各衛星を出発したマイクロ波（約1.2GHz及び1.6GHz）が受信機に到達するまでに伝播した時間（距離）を測定し，各衛星の位置を基準にして，受信機の位置を求める．マイクロ波は，地表付近で電離層や対流圏に遭遇するが（図2），このとき，屈折率の関係で速度や経路が変化して伝搬が遅れ，距離測定に影響を及ぼす．天頂方向の遅延量は，電離層で1〜10m程度，対流圏で2.5m程度であるが，衛星の天頂角z が大きくなるにつれて遅延量も概ね1/cos(z )の割合で大きくなるので，補正が必要である[3]．

　電離層遅延は，マイクロ波の周波数に依存するので，2周波データの組み合わせにより消去できる．しかし（周波数に依存しない）対流圏遅延は残るので，適切な理論式により補正するか，未知パラメータとして推定する必要がある．

　大気の物理に関する考察から，様々な対流圏遅延の理論式が作られているが，いずれも天頂方向の遅延量に，天頂角（仰角）に依存するマッピング関数をかけた形で表される．通常のGPS測量では，こうした理論式を用いて対流圏遅延を補正する．相対測位なので，距離が短ければ各観測点での遅延量はほぼ相殺され，そこそこに良い測位精度が得られる．しかし，最高精度が要求される地殻変動観測では，各点の天頂方向の対流圏遅延量を，例えば3時間毎に一定値としてモデル化し，それらも座標と一緒に最小二乗法により推定する．この際，対流圏遅延は短い時間では余り変化しないので，時間変化に拘束条件をつけることもある．さらに，これを発展させた手法が，対流圏遅延の時系列を確率過程として取り扱い，カルマンフィルターによって解く手法である[4]．

　このような工夫により測位精度は向上するが，それでも推定された対流圏遅延量と座標の上下成分（高さ）との間には高い相関があり，対流圏遅延が厄介な誤差要因であることに変わりはない．例えば，現実の大気状態とマッピング関数との矛盾は，高さに系統誤差を与えてしまうであろう．